
分析 (1)取x=y=0,求出f(0)的值,代入证明即可;
(2)求出k,构造函数g(x)=max{-x,2x-x2},由-x>2x-x2?x<0,或x>3,得到关于k的二次函数,求出u的范围即可.
解答 解:(1)f(x)在R递增,
证明如下:取x=y=0得:f(0+0)=f(0)+f(0)+$\frac{1}{2}$,解得:f(0)=-$\frac{1}{2}$,
任取x1,x2∈R,且x1<x2,
则f(x2)-f(x1)=f((x2-x1)+x1)-f(x1)
=f(x2-x1)+f(x1)+$\frac{1}{2}$-f(x1)=f(x2-x1)+$\frac{1}{2}$>0,
∵x2-x1>0,∴f(x2-x1)>-$\frac{1}{2}$,
∴f(x1)<f(x2),
∴函数f(x)在R递增;
(2)由F(x)=0?f(max{-x,2x-x2})+f(-k)+1=0
?f(max{-x,2x-x2})+f(-k)+$\frac{1}{2}$=-$\frac{1}{2}$
?f(max{-x,2x-x2}+(-k))=f(0),
而f(x)在R递增,
∴f(max{-x,2x-x2}+(-k))=f(0)?max{-x,2x-x2}+(-k)=0
?k=max{-x,2x-x2},
构造函数g(x)=max{-x,2x-x2},由-x>2x-x2?x<0,或x>3,
∴g(x)=$\left\{\begin{array}{l}{-x,x∈(-∞,0)∪(3,+∞)}\\{2x{-x}^{2},x∈[0,3]}\end{array}\right.$,
于是,结合题意得:
y=k与y=g(x)的图象有3个不同的交点,
不妨设这3个零点为:x1<x2<x3,
则0<k<1,x1=-k,x2,x3是方程2x-x2=k的两根,
即x2,x3的方程x2-2x+k=0的两根,
∴$\left\{\begin{array}{l}{{x}_{2}{+x}_{3}=2}\\{{x}_{2}{•x}_{3}=k}\end{array}\right.$,
∴u=(x1+x2+x3)+x1x2x3=2-k-k2=$\frac{9}{4}$-${(k+\frac{1}{2})}^{2}$在k∈(0,1)递减,
故0<u<2.
点评 不同考查了函数的单调性、最值问题,考查转化思想,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | a,b,c成等比数列 | B. | a,b,c成等差数列 | C. | a,c,b成等比数列 | D. | a,c,b成等差数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
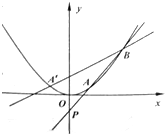 已知抛物线C:x2=2py(p>0)过点(2,1),直线l过点P(0,-1)与抛物线C交于A、B两点,点A关于y轴的对称点为A′,连接A′B
已知抛物线C:x2=2py(p>0)过点(2,1),直线l过点P(0,-1)与抛物线C交于A、B两点,点A关于y轴的对称点为A′,连接A′B查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 4 | C. | 8(log23-1) | D. | $-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com