
分析 (1)由椭圆的离心率求得a=$\sqrt{2}$c,根据勾股定理及椭圆的定义,求得a-c=$\sqrt{2}$-1.b2=a2-c2=1,即可求得椭圆的标准方程;
(2)设直线l的方程,代入椭圆方程,由韦达定理及弦长公式求得丨AB丨,由两平行之间的距离公式,由矩形的周长公式2(丨AB丨+d)=$\frac{11\sqrt{2}}{3}$,代入即可求得m的值,求得直线AB的方程.
解答 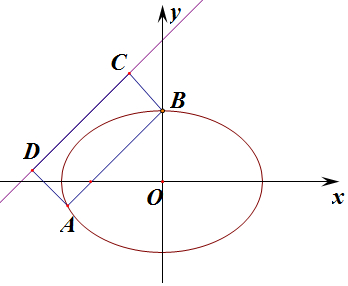 解:(1)∵离心率为e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,则a=$\sqrt{2}$c,①
解:(1)∵离心率为e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,则a=$\sqrt{2}$c,①
由PF1⊥PF2,则丨PF1丨2+丨PF2丨2=丨F1F2丨2=4c2,
由椭圆的定义可知;丨PF1丨+丨PF2丨=2a,则丨F1F2丨2=(丨PF1丨+丨PF2丨)2-2丨PF1丨•丨PF2丨,
∴丨PF1丨•丨PF2丨=2a2-2c2,
,△PF1F2的面积S,S=$\frac{1}{2}$丨PF1丨•丨PF2丨=$\frac{1}{2}$×R×(丨PF1丨+丨PF2丨+丨F1F2丨),
则a-c=$\sqrt{2}$-1.②
由①②解得:a=$\sqrt{2}$,c=1,
b2=a2-c2=1,
∴椭圆E的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(2)由题意设直线l的方程:y=x+m,A(x1,y1)、B(x2,y2),
则$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,整理得:3x2+4mx+2m2-2=0,
由△=16m2-4×3(2m2-2)=-2m2+3>0,解得-$\sqrt{3}$<m<$\sqrt{3}$,
由韦达定理可知:x1+x2=-$\frac{4m}{3}$,x1x2=$\frac{2{m}^{2}-2}{3}$,
则丨AB丨=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}$•$\sqrt{(-\frac{4m}{3})^{2}-4×\frac{2{m}^{2}-2}{3}}$=$\frac{4\sqrt{3-{m}^{2}}}{3}$,
直线AB,CD之间的距离d=$\frac{丨m-2丨}{\sqrt{1+1}}$=$\frac{\sqrt{2}丨m-2丨}{2}$,
由矩形ABCD的周长为$\frac{11\sqrt{2}}{3}$,则2(丨AB丨+d)=$\frac{11\sqrt{2}}{3}$,
则2($\frac{4\sqrt{3-{m}^{2}}}{3}$+$\frac{\sqrt{2}丨m-2丨}{2}$)=$\frac{11\sqrt{2}}{3}$,解得:m=1,
则直线AB的方程为y=x+1.
点评 本题考查椭圆方程标准方程及简单几何性质,直线与椭圆的位置关系,韦达定理及弦长公式,考查推理论证能力、运算求解能力,考查等价转化思想,难度大,对数学思维能力要求较高,属于中档题.


科目:高中数学 来源: 题型:选择题
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,为了研究某城市2016年的空气质量情况,省环保局从全年的检测数据中随机抽取了30天进行统计,得到茎叶图如图所示,则该样本的中位数、众数、极差分别是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,为了研究某城市2016年的空气质量情况,省环保局从全年的检测数据中随机抽取了30天进行统计,得到茎叶图如图所示,则该样本的中位数、众数、极差分别是( )| A. | 76,75,56 | B. | 76,75,53 | C. | 77,75,56 | D. | 75,77,53 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | ±4 | C. | 4$\sqrt{3}$ | D. | ±4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | i | D. | -i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | n<2017 | B. | n≤2017 | C. | n>2017 | D. | n≥2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{3}$,$\frac{\sqrt{3}}{3}$] | B. | [$\frac{1}{3}$,+∞) | C. | [$\frac{\sqrt{3}}{3}$,+∞) | D. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
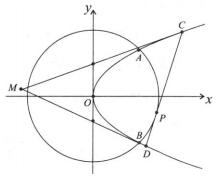 如图,已知抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.
如图,已知抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com