
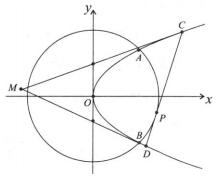
 如图,已知抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.
如图,已知抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.分析 (1)由2pxA=4,p=1.即可求得p的值,求得抛物线方程;
(2)分别求得直线l1,l2方程,联立,求得交点M坐标,求得足$x_0^2+y_0^2=8$,${x_0}∈[{2,2\sqrt{2}}]$,利用点到直线的距离公式,根据函数的单调性即可求得点M到直线CD距离的最大值.
解答 解:(1)由xA=2得$y_A^2=4$,故2pxA=4,p=1.
于是,抛物线E的方程为y2=2x.
(2)设$C({\frac{y_1^2}{2},{y_1}})$,$D({\frac{y_2^2}{2},{y_2}})$,切线l1:$y-{y_1}=k({x-\frac{y_1^2}{2}})$,
代入y2=2x得$k{y^2}-2y+2{y_1}-ky_1^2=0$,由△=0解得$k=\frac{1}{y_1}$,
∴l1方程为$y=\frac{1}{y_1}x+\frac{y_1}{2}$,同理l2方程为$y=\frac{1}{y_2}x+\frac{y_2}{2}$,
联立$\left\{\begin{array}{l}y=\frac{1}{y_1}x+\frac{y_1}{2}\\ y=\frac{1}{y_2}x+\frac{y_2}{2}\end{array}\right.$,解得$\left\{\begin{array}{l}x=\frac{{{y_1}•{y_2}}}{2}\\ y=\frac{{{y_1}+{y_2}}}{2}\end{array}\right.$,
易得CD方程为x0x+y0y=8,其中x0,y0满足$x_0^2+y_0^2=8$,${x_0}∈[{2,2\sqrt{2}}]$,
联立方程$\left\{\begin{array}{l}{y^2}=2x\\{x_0}x+{y_0}y=8\end{array}\right.$得${x_0}{y^2}+2{y_0}y-16=0$,则$\left\{\begin{array}{l}{y_1}+{y_2}=-\frac{{2{y_0}}}{x_0}\\{y_1}•{y_2}=-\frac{16}{x_0}\end{array}\right.$,
∴M(x,y)满足$\left\{\begin{array}{l}x=-\frac{8}{x_0}\\ y=-\frac{y_0}{x_0}\end{array}\right.$,即点M为$(-\frac{8}{x_0},-\frac{y_0}{x_0})$.
点M到直线CD:x0x+y0y=8的距离$d=\frac{{|{-8-\frac{y_0^2}{x_0}-8}|}}{{\sqrt{x_0^2+y_0^2}}}=\frac{{\frac{y_0^2}{x_0}+16}}{{2\sqrt{2}}}=\frac{{\frac{8-x_0^2}{x_0}+16}}{{2\sqrt{2}}}=\frac{{\frac{8}{x_0}-{x_0}+16}}{{2\sqrt{2}}}$,
关于x0单调减,
故当且仅当x0=2时,${d_{max}}=\frac{18}{{2\sqrt{2}}}=\frac{{9\sqrt{2}}}{2}$.
点评 本题考查直线与抛物线的位置关系,考查点到直线的距离公式,函数单调性与抛物线的综合应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题¬q:?x∈R,x2≤0为假命题 | B. | 命题¬q:?x∈R,x2≤0为真命题 | ||
| C. | 命题¬q:?x∈R,x2≤0为假命题 | D. | 命题¬q:?x∈R,x2≤0为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈[-2,+∞),x0+3<1 | B. | ?x0∈[-2,+∞),x0+3≥1 | ||
| C. | ?0∈[-2,+∞),x0+3<1 | D. | ?x0∈(-∞,-2),x0+3≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{π}{6},\frac{π}{2}]$ | B. | $[\frac{π}{4},\frac{π}{3}]$ | C. | $[\frac{π}{3},\frac{π}{2}]$ | D. | $[\frac{π}{6},\frac{π}{4}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com