练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知圆C经过直线与坐标轴的两个交点，且经过抛物线的焦点，则圆C的方程为 ．

     

    .

    【解析】

    试题分析：与坐标轴的两个交点是：（4，0），（0,2），抛物线的焦点是（2,0），所以可以设圆的一般方程，把上面三个点坐标带入，解得D=-6，E=-6，F=8.

    考点：求圆的方程.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届江西南昌市四校高二上学期期末联考理科数学试卷（解析版） 题型：解答题

    在数列{}中，已知

    （1）求并由此猜想数列{}的通项公式的表达式；

    （2）用数学归纳法证明你的猜想。

     

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省常州市高二上学期期末考试理科数学试卷（解析版） 题型：解答题

    已知圆.

    （1）若直线过点，且与圆相切，求直线的方程；

    （2）若圆的半径为4，圆心在直线：上，且与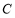圆内切，求圆 的方程．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省常州市高二上学期期末考试理科数学试卷（解析版） 题型：填空题

    命题“若，则”的否命题为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省常州市高二上学期期末考试理科数学试卷（解析版） 题型：填空题

    已知椭圆：的短轴长为2，离心率为，设过右焦点的直线与椭圆交于不同的两点A，B，过A，B作直线的垂线AP，BQ，垂足分别为P，Q．记， 若直线l的斜率≥,则的取值范围为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省常州市高二上学期期末考试理科数学试卷（解析版） 题型：填空题

    圆心为，且经过点的圆的标准方程为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省常州市高二上学期期末考试文科数学试卷（解析版） 题型：解答题

    已知抛物线的焦点为双曲线的一个焦点，且两条曲线都经过点.

    （1）求这两条曲线的标准方程；

    （2）已知点在抛物线上，且它与双曲线的左，右焦点构成的三角形的面积为4，求点 的坐标.

     

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省仪征市高二第一学期期末考试数学试卷（解析版） 题型：解答题

    某地政府为科技兴市，欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区（如图中阴影部分），形状为直角梯形QPRE（线段EQ和RP为两个底边），已知其中AF是以A为顶点、AD为对称轴的抛物线段．试求该高科技工业园区的最大面积．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏扬州市高二第一学期期末调研考试数学试卷（解析版） 题型：解答题

    如图，储油灌的表面积为定值，它的上部是半球，下部是圆柱，半球的半径等于圆柱底面半径．

    ⑴试用半径表示出储油灌的容积，并写出的范围．

    ⑵当圆柱高与半径的比为多少时，储油灌的容积最大？

     

    查看答案和解析>>

    同步练习册答案