
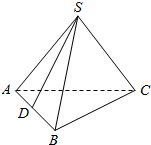
 如图,在正四面体S-ABC(四个面都是等边三角形)中,点D是棱AB的中点,则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$.
如图,在正四面体S-ABC(四个面都是等边三角形)中,点D是棱AB的中点,则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$. 分析 取AC中点E,连接DE、SE.在△ABC中利用中位线定理得DE∥BC,所以∠SDE(或其补角)即为异面直线SD与BC所成的角,设正四面体棱长为a,算出△SDE中各边之长,再利用余弦定理加以计算可得答案.
解答  解:取AC中点E,连接DE、SE,
解:取AC中点E,连接DE、SE,
∵△ABC中D,E分别为AB、AC的中点,∴DE∥BC,DE=$\frac{1}{2}$BC
因此,∠SDE(或其补角)即为异面直线SD与BC所成的角,
设正四面体棱长为a,由题意可得SD=SE=$\frac{\sqrt{3}}{2}$a,DE=$\frac{1}{2}$a,
∴在△SDE中,根据余弦定理得
cos∠SDE=$\frac{D{E}^{2}+S{D}^{2}-S{E}^{2}}{2DE×SD}$=$\frac{\frac{1}{4}{a}^{2}+\frac{3}{4}{a}^{2}-\frac{3}{4}{a}^{2}}{2×\frac{1}{2}a×\frac{\sqrt{3}}{2}a}$=$\frac{\sqrt{3}}{6}$
即异面直线AE和BD所成角的余弦值为 $\frac{\sqrt{3}}{6}$;
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题在正四面体中求异面直线所成角大小.着重考查了正四面体的性质、三角形的中位线定理和异面直线所成角的定义及其求法等知识,属于中档题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
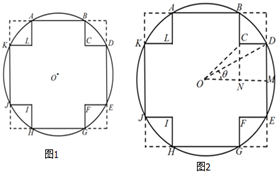 如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)
如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一切奇数都属于S | B. | 偶数4k-2(k∈Z)都不属于S | ||
| C. | 若x,y∈S,则xy∈S | D. | 若x,y属于S,则x+y∈S |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10≤x≤20 | B. | 10≤x≤30 | C. | 20≤x≤40 | D. | 10≤x≤50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F.
如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com