
| A. | 一切奇数都属于S | B. | 偶数4k-2(k∈Z)都不属于S | ||
| C. | 若x,y∈S,则xy∈S | D. | 若x,y属于S,则x+y∈S |
分析 由已知S是好集,得到集合元素的属性,由此分别分析选项.
解答 解:因为S是一个“好集”,
所以S中的任何元素都满足a2-b2∈S,由a2-b2=(a+b)(a-b),
因为奇数+偶数=奇数,奇数-偶数=奇数,奇数×奇数=奇数,所以A正确;
对于B,4k-2=2(2k-1),是偶数×奇数的形式,所以4k-2∉S;故B正确;
对于C,x∈S,y∈S,设x=a2-b2,y=c2-d2,则xy=(a2-b2)(c2-d2)=(ac)2-(ad)2-(bc)2+(bd)2∈S;故C正确;
对于D,x∈S,y∈S,设x=a2-b2,y=c2-d2,则x+y=(a2-b2)+(c2-d2)=(a2+c2)-(b2+d2)∉S;故D错误;
故选C.
点评 本题考查了集合与元素的关系,关键是明确对好集定义的理解.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | λ=$\frac{5}{4}$,μ=$\frac{3}{4}$ | B. | λ=$\frac{4}{3}$,μ=$\frac{5}{6}$ | C. | λ=$\frac{5}{3}$,μ=$\frac{7}{6}$ | D. | λ=$\frac{4}{3}$,μ=$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a⊥β | B. | b⊥α | ||
| C. | a⊥β与b⊥α中至少有一个成立 | D. | a⊥β与b⊥α同时成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$ | B. | $\frac{{a}^{2}}{b}$ | C. | $\frac{b}{a}$ | D. | $\frac{{b}^{2}}{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
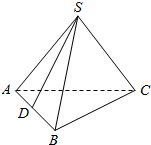 如图,在正四面体S-ABC(四个面都是等边三角形)中,点D是棱AB的中点,则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$.
如图,在正四面体S-ABC(四个面都是等边三角形)中,点D是棱AB的中点,则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com