
���� ����������õ�a��b�Ĺ�ϵ���õ���ԲC�ķ���Ϊ$\frac{{x}^{2}}{3{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$���ѵ�P��$\frac{\sqrt{3}}{2}$��$\frac{\sqrt{3}}{2}$���������b2=1��������a2=3������Բ���̿���
������ֱ��l��б�ʲ�����ʱ��������l�ķ���Ϊx=1������$\frac{{x}^{2}}{3}+{y}^{2}=1$�����|MN|=$\frac{2\sqrt{6}}{3}$��$\sqrt{3}$���������⣮��ֱ��l��б�ʴ���ʱ����l�ķ���Ϊy=kx+m�������⣬��$\frac{|m|}{\sqrt{1+{k}^{2}}}=1$�õ�m��k�Ĺ�ϵ������ֱ�߷��̺���Բ���̣����ҳ���ʽ�õ�|MN|=$\frac{2\sqrt{6}|k|\sqrt{1+{k}^{2}}}{1+3{k}^{2}}=\sqrt{3}$���ⷽ�����k��ֵ��
��� �⣺���������⣬��e2=1-$\frac{{b}^{2}}{{a}^{2}}$=$\frac{2}{3}$����a2=3b2������ԲC�ķ���Ϊ$\frac{{x}^{2}}{3{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$��
�ߵ�P��C�ϣ�����P��$\frac{\sqrt{3}}{2}$��$\frac{\sqrt{3}}{2}$����������룬��b2=1������a2=3��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{3}+{y}^{2}=1$��
����ֱ��l��б�ʲ�����ʱ��������l�ķ���Ϊx=1������$\frac{{x}^{2}}{3}+{y}^{2}=1$��
��M��1��$\frac{\sqrt{6}}{3}$����N��1��-$\frac{\sqrt{6}}{3}$����|MN|=$\frac{2\sqrt{6}}{3}$��$\sqrt{3}$���������⣮
��ֱ��l��б�ʴ���ʱ����l�ķ���Ϊy=kx+m��
�����⣬��$\frac{|m|}{\sqrt{1+{k}^{2}}}=1$����m2=k2+1��
��y=kx+m����$\frac{{x}^{2}}{3}+{y}^{2}=1$���ã�1+3k2��x2+6kmx+3m2-3=0��
��M��x1��y1����N��x2��y2������x1+x2=$\frac{-6km}{1+3{k}^{2}}$��x1x2=$\frac{3{m}^{2}-3}{1+3{k}^{2}}$��
��|MN|=$\sqrt{1+{k}^{2}}|{x}_{1}-{x}_{2}|=\sqrt{1+{k}^{2}}\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$��$\frac{2\sqrt{3��3{k}^{2}+1-{m}^{2}��}}{1+3{k}^{2}}$
=$\frac{2\sqrt{6}|k|\sqrt{1+{k}^{2}}}{1+3{k}^{2}}=\sqrt{3}$����������k4-2k2+1=0�����k2=1��k=��1��
���ϣ���ֱ֪��l��б��Ϊ��1��
���� ���⿼������Բ���̵���������ֱ�ߺ�Բ���ߵ�λ�ù�ϵ��ѵ�����ҳ���ʽ��Ӧ�ã����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ������������S | B�� | ż��4k-2��k��Z����������S | ||
| C�� | ��x��y��S����xy��S | D�� | ��x��y����S����x+y��S |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ABC��A��7��8����B��3��5����C��4��3����M��N��D�ֱ���AB��AC��BC���е㣬��MN��AD����F��
��ͼ����֪��ABC��A��7��8����B��3��5����C��4��3����M��N��D�ֱ���AB��AC��BC���е㣬��MN��AD����F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
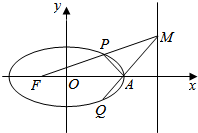 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����ΪF��-1��0����MΪ����x=4�ϵ�һ���㣨����x���ϣ����߶�FM����Բ�ڵ�P��MA����Բ����һ����ΪQ��
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����ΪF��-1��0����MΪ����x=4�ϵ�һ���㣨����x���ϣ����߶�FM����Բ�ڵ�P��MA����Բ����һ����ΪQ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+2y-8=0 | B�� | 2x-y-8=0 | C�� | x+2y-4=0 | D�� | 2x-y=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6��310-1�� | B�� | $\frac{1}{6}$��310-1�� | C�� | 6��1-310�� | D�� | $\frac{1}{6}$��1-310�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com