
| A. | $\frac{1}{6}$ | B. | $\frac{1}{7}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{9}$ |
分析 由ln(x2+1)等于0,1,2求解对数方程分别得到x的值,然后利用列举法得到值域为{0,1,2}的所有定义域情况,则满足条件的函数个数可求,由此利用等可能事件概率计算公式能求出取出的2个集合中各有三个元素的概率.
解答 解:令ln(x2+1)=0,得x=0,
令ln(x2+1)=1,得x2+1=e,x=±$\sqrt{e-1}$,
令ln(x2+1)=2,得x2+1=e2,x=$±\sqrt{{e}^{2}-1}$.
则满足值域为{0,1,2}的定义域有:
{0,-$\sqrt{e-1}$,-$\sqrt{{e}^{2}-1}$},{0,-$\sqrt{e-1}$,$\sqrt{{e}^{2}-1}$},{0,$\sqrt{e-1}$,-$\sqrt{{e}^{2}-1}$},
{0,$\sqrt{e-1}$,$\sqrt{{e}^{2}-1}$},{0,-$\sqrt{e-1}$,$\sqrt{e-1}$,-$\sqrt{{e}^{2}-1}$},{0,-$\sqrt{e-1}$,$\sqrt{e-1}$,$\sqrt{{e}^{2}-1}$},
{0,-$\sqrt{e-1}$,-$\sqrt{{e}^{2}-1}$,$\sqrt{{e}^{2}-1}$},{0,$\sqrt{e-1}$,-$\sqrt{{e}^{2}-1}$,$\sqrt{{e}^{2}-1}$},
{0,-$\sqrt{e-1}$,$\sqrt{e-1}$,-$\sqrt{{e}^{2}-1}$,$\sqrt{{e}^{2}-1}$}.
则满足这样条件的函数的个数为9.
从满足条件的所有定义域集合中选出2个集合,
基本事件总数n=${C}_{9}^{2}=36$,
取出的2个集合中各有三个元素的函数个数为m=${C}_{4}^{2}=6$,
∴取出的2个集合中各有三个元素的概率是p=$\frac{m}{n}=\frac{1}{6}$.
故选:A.
点评 本小题主要考查学生对概率统计知识的理解,以及函数的相关知识,同时考查学生的数据处理能力,是中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{11}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{23}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | [1,3] | C. | [1,4] | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
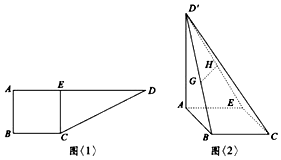 如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D'EC的位置,使$D'A=2\sqrt{3}$,如图<2>:若G,H分别为D'B,D'E的中点.
如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D'EC的位置,使$D'A=2\sqrt{3}$,如图<2>:若G,H分别为D'B,D'E的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com