
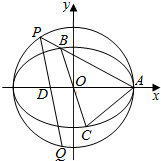
 ��ͼ����ƽ��ֱ������ϵxOy�У���֪ԲO��x2+y2=4����ԲC��$\frac{x^2}{4}+{y^2}=1$��AΪ��Բ�Ҷ��㣮��ԭ��O�������������ֱ������ԲC����B��C���㣬ֱ��AB��ԲO����һ����ΪP��ֱ��PD��ԲO����һ����ΪQ������$D��-\frac{6}{5}��0��$����ֱ��AB��AC��б�ʷֱ�Ϊk1��k2��
��ͼ����ƽ��ֱ������ϵxOy�У���֪ԲO��x2+y2=4����ԲC��$\frac{x^2}{4}+{y^2}=1$��AΪ��Բ�Ҷ��㣮��ԭ��O�������������ֱ������ԲC����B��C���㣬ֱ��AB��ԲO����һ����ΪP��ֱ��PD��ԲO����һ����ΪQ������$D��-\frac{6}{5}��0��$����ֱ��AB��AC��б�ʷֱ�Ϊk1��k2������ ��1����B��x0��y0������C��-x0��-y0����������Բ���̣�����ֱ�ߵ�б�ʹ�ʽ�����ɵõ�����ֵ��
��2������ֱ��AB�ķ��̺�Բ���̣����P�����ꣻ����ֱ��AB�ķ��̺���Բ���̣����B�����꣬����ֱ��PQ����ֱ��BC��б�ʣ����ɵõ����ۣ�
��3������ֱ��PQ��б�ʲ����ںʹ��ڣ�����ֱ��PQ�ķ��̺���Բ���̣����Q�����꣬�ɵ�AQ��б�ʣ����ɵ�֤��
��� �⣺��1����B��x0��y0������C��-x0��-y0����$\frac{{{x_0}^2}}{4}+{y_0}^2=1$��
����${k_1}{k_2}=\frac{y_0}{{{x_0}-2}}•\frac{y_0}{{{x_0}+2}}=\frac{{{y_0}^2}}{{{x_0}^2-4}}=\frac{{1-\frac{1}{4}{x_0}^2}}{{{x_0}^2-2}}=-\frac{1}{4}$��
��2������$\left\{\begin{array}{l}y={k_1}��x-2��\\{x^2}+{y^2}=4\end{array}\right.$��$��1+k_1^2��{x^2}-4k_1^2x+4��k_1^2-1��=0$��
���${x_P}=\frac{2��k_1^2-1��}{1+k_1^2}��{y_P}={k_1}��{x_P}-2��=\frac{{-4{k_1}}}{1+k_1^2}$��
����$\left\{\begin{array}{l}y={k_1}��x-\sqrt{2}��\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$��$��1+4k_1^2��{x^2}-16k_1^2x+4��4k_1^2-1��=0$��
���${x_B}=\frac{2��4k_1^2-1��}{1+4k_1^2}��{y_B}={k_1}��{x_B}-\sqrt{2}��=\frac{{-4{k_1}}}{1+4k_1^2}$��
����${k_{BC}}=\frac{y_B}{x_B}=\frac{{-2{k_1}}}{4k_1^2-1}$��${k_{PQ}}=\frac{y_P}{{{x_P}+\frac{6}{5}}}=\frac{{\frac{{-4{k_1}}}{1+k_1^2}}}{{\frac{2��k_1^2-1��}{1+k_1^2}+\frac{6}{5}}}=\frac{{-5{k_1}}}{4k_1^2-1}$��
����${k_{PQ}}=\frac{5}{2}{k_{BC}}$��
�ʴ��ڳ���$��=\frac{5}{2}$��ʹ��${k_{PQ}}=\frac{5}{2}{k_{BC}}$��
��3��֤������ֱ��PQ��x�ᴹֱʱ��$Q��-\frac{6}{5}��-\frac{8}{5}��$��
��${k_{AQ}}=\frac{{-\frac{8}{5}}}{{-\frac{6}{5}-2}}=\frac{1}{2}={k_2}$������ֱ��AC�ع���Q��
��ֱ��PQ��x���ֱʱ��ֱ��PQ����Ϊ��$y=\frac{{-5{k_1}}}{4k_1^2-1}��x+\frac{6}{5}��$��
����$\left\{\begin{array}{l}y=\frac{{-5{k_1}}}{4k_1^2-1}��x+\frac{6}{5}��\\{x^2}+{y^2}=4\end{array}\right.$��
���${x_Q}=\frac{-2��16k_1^2-1��}{16k_1^2+1}��{y_Q}=\frac{{16{k_1}}}{16k_1^2+1}$��
����${k_{AQ}}=\frac{{\frac{{16{k_1}}}{16k_1^2+1}}}{{\frac{-2��16k_1^2-1��}{16k_1^2+1}-2}}=-\frac{1}{{4{k_1}}}={k_2}$��
��ֱ��AC�ع���Q��
���� ���⿼����Բ�ķ��̺����ʣ�����ֱ�߷��̺���Բ������������ý��㣬����ֱ�ߵ�б�ʺͷ��̵����ã��ͻ������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-1��0��1} | B�� | {-1��1} | C�� | {-1��1��2} | D�� | {1��0} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
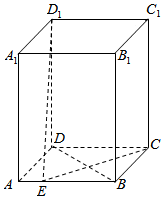 ��ͼ����������ABCD-A1B1C1D1�У�����ABCD�������Σ�����AA1�͵���ABCD����֪AB=1��${A}{{A}_1}=\sqrt{3}$��EΪAB��һ�����㣬��D1E+CE����СֵΪ��������
��ͼ����������ABCD-A1B1C1D1�У�����ABCD�������Σ�����AA1�͵���ABCD����֪AB=1��${A}{{A}_1}=\sqrt{3}$��EΪAB��һ�����㣬��D1E+CE����СֵΪ��������| A�� | $2\sqrt{2}$ | B�� | $\sqrt{10}$ | C�� | $\sqrt{5}+1$ | D�� | $2+\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij�������ŶԸ������ij�����4�괺���ڼ䣨ÿ���ͳ�ƴ��ڼ��ڵ�ǰ7�죩�Ŀ�����Ⱦָ��������ͳ�Ʒ������Ұ��Ƿ�ȼ�ű��ڷֳ����飬�õ���ͼ�ľ�Ҷͼ�����ݹ������±���������Ⱦָ��������100�ı�ʾû������������100�ı�ʾ��������
ij�������ŶԸ������ij�����4�괺���ڼ䣨ÿ���ͳ�ƴ��ڼ��ڵ�ǰ7�죩�Ŀ�����Ⱦָ��������ͳ�Ʒ������Ұ��Ƿ�ȼ�ű��ڷֳ����飬�õ���ͼ�ľ�Ҷͼ�����ݹ������±���������Ⱦָ��������100�ı�ʾû������������100�ı�ʾ��������| ȼ�� | δȼ�� | �ϼ� | |
| ������ | |||
| ������ | |||
| �ϼ� |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | 16 | 17 | 18 | 19 |
| y | 50 | 34 | 41 | 31 |
| A�� | 26�� | B�� | 27�� | C�� | 28�� | D�� | 29�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com