
分析 (Ⅰ)由f(0)=1,得a=2,函数f(x)=log2(2x+1)+bx的图象关于y轴对称⇒f(x)=f(-x)求得b
(Ⅱ)函数g(x)=f(x)-$\frac{1}{2}$x+c在[0,1]上存在零点?即方程log2(2x+1)-x=-c在[0,1]上有解,
g(x)=log2(2x+1)-x与y=-c由交点,
(Ⅲ)函数φ(x)=2f(2x)+x+λ×2x-1=4x+1+λ•2x-1=4x+λ•2x
令t=2x,h(t)=t2+λt,t∈[$\frac{1}{2}$,4]
结合二次函数图象,分类求最小值即可.
解答 解:(Ⅰ)∵函数f(x)=loga(ax+1)+bx(a>0且a≠1,b∈R)满足f(0)=1,∴a=2
函数f(x)=log2(2x+1)+bx的图象关于y轴对称⇒log2(2x+1)+bx=log2(2-x+1)-bx
⇒2bx=bx=log2(2-x+1)-log2(2x+1)=log22-x=-x,∴b=-$\frac{1}{2}$
综上a=2,b=-$\frac{1}{2}$.
(Ⅱ)函数g(x)=f(x)-$\frac{1}{2}$x+c在[0,1]上存在零点?方程log2(2x+1)-x+c=0在[0,1]上有解,
即方程log2(2x+1)-x=-c在[0,1]上有解,
令g(x)=log2(2x+1)-x=log2$\frac{{2}^{x}+1}{{2}^{x}}$=log2(1+$\frac{1}{{2}^{x}}$)$∈[lo{g}_{2}\frac{3}{2},1]$,
∴-1≤c≤-log2$\frac{3}{2}$⇒实数c的取值范围为[-1,-log2$\frac{3}{2}$]
(Ⅲ)函数φ(x)=2f(2x)+x+λ×2x-1=4x+1+λ•2x-1=4x+λ•2x
令t=2x,h(t)=t2+λt,t∈[$\frac{1}{2}$,4]
故当-$\frac{λ}{2}$≤$\frac{1}{2}$,即λ≥-1时,当t=$\frac{1}{2}$,函数的最小值$\frac{1}{4}+\frac{1}{2}λ=-1$,⇒λ=-$\frac{5}{2}$(舍去);
当$\frac{1}{2}<-\frac{λ}{2}<4,即-8<λ<-1$,t=-$\frac{λ}{2}$时,函数最小值为$\frac{-{λ}^{2}}{4}=-1解得λ=-2或2(舍去)$;
当$-\frac{λ}{2}≥4,即λ≤-8时$,当t=4时,函数最小值为12+4λ=-1,解得$λ=-\frac{13}{4}$(舍去)
综上:存在实数λ=-2使得φ(x)的最小值为-1.
点评 本题考查了对数函数型、指数函数型的函数运算与性质,含参数二次函数最值问题,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 5 | C. | -5 | D. | ±5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2,3} | B. | {-1,0,1} | C. | {y|-1≤y≤1} | D. | {y|0≤y≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
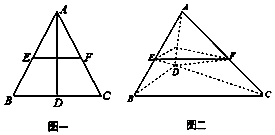 如图一,在边长为2的等边三角形ABC中,D、E、F分别是BC、AB、AC的中点,将△ABD沿AD折起,得到如图二所示的三棱锥A-BCD,其中$BC=\sqrt{2}$.
如图一,在边长为2的等边三角形ABC中,D、E、F分别是BC、AB、AC的中点,将△ABD沿AD折起,得到如图二所示的三棱锥A-BCD,其中$BC=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com