练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知全集U={1，2，3}，集合A={1}，B={2}，则∁U（A∪B）=（　　）
    A．∅B．UC．{1，2}D．{3}

    分析 根据并集和补集的定义写出运算结果即可．

    解答 解：全集U={1，2，3}，集合A={1}，B={2}，
    则A∪B={1，2}，
    所以∁U（A∪B）={3}．
    故选：D．

    点评 本题考查了集合的定义与运算问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015-2016学年河南省商丘市高一文下学期期末考数学试卷（解析版） 题型：选择题

    若向量两两所成的角相等，且则等于（ ）

    A．2 B． C． D．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年河北省保定市高一上学期期中考试数学试卷（解析版） 题型：选择题

    已知集合A={2，3}，B={x|mx﹣6=0}，若B⊆A，则实数m=（ ）

    A．3 B．2

    C．2或3 D．0或2或3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知两定点A（-2，0），B（1，0），若圆心在直线x-y-1=0上且半径为1的动圆P上存在一点Q满足|QA|=2|QB|，则点P横坐标a的取值范围为$\frac{3-\sqrt{17}}{2}≤a≤1$或2≤a≤$\frac{3+\sqrt{17}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在直角坐标系xoy中，圆C的参数方程为$\left\{\begin{array}{l}x=2+2cosφ\\ y=2sinφ\end{array}\right.$（φ为参数），以O为极点，x轴的非负半轴为极轴建立极坐标系．
    （1）求圆C的极坐标方程；
    （2）若直线$l：\left\{\begin{array}{l}x=m+\frac{{\sqrt{3}}}{2}t\\ y=\frac{1}{2}t\end{array}\right.$（t为参数）与圆C交于A，B两点，且$|{AB}|=\sqrt{15}$，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象与直线y=b（0＜b＜A）的三个相邻交点的横坐标分别是1，2，4，则f（x）的单调递增区间是（　　）
    A．[3k-$\frac{3}{2}$，3k]，k∈ZB．[3k，3k+$\frac{3}{2}$]，k∈ZC．[3kπ-$\frac{3}{2}$，3kπ]，k∈ZD．[3kπ，3kπ+$\frac{3}{2}$]，k∈Z

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．如图，是一个几何体的三视图，则此几何体的外接球的半径为（　　）
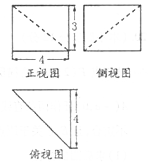
    A．$\frac{\sqrt{34}}{2}$B．$\frac{\sqrt{41}}{2}$C．17D．41

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．过双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点F作x轴的垂线，交双曲线C于M，N两点，A为左顶点，设∠MAN=θ，双曲线C的离心率为f（θ），则f（$\frac{2π}{3}$）-f（$\frac{π}{3}$）等于（　　）
    A．$\frac{2\sqrt{3}}{3}$B．$\frac{\sqrt{3}}{3}$C．$\sqrt{3}$D．$\frac{\sqrt{6}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．某公司2017年元旦晚会现场，为了活跃气氛，将在晚会节目表演过程中进行抽奖活动．
    （1）现需要从第一排就座的6位嘉宾A、B、C、D、E、F中随机抽取2人上台抽奖，求嘉宾A和嘉宾B至少有一人上台抽奖的概率；
    （2）抽奖活动的规则是：嘉宾通过操作按键使电脑自动产生两个[0，1]之间的随机数x，y，并按如图所示的程序框图执行．若电脑显示“中奖”，则该嘉宾中奖；若电脑显示“谢谢”，则不中奖．求该嘉宾中奖的概率．

    查看答案和解析>>

    同步练习册答案