
| A. | [3k-$\frac{3}{2}$,3k],k∈Z | B. | [3k,3k+$\frac{3}{2}$],k∈Z | C. | [3kπ-$\frac{3}{2}$,3kπ],k∈Z | D. | [3kπ,3kπ+$\frac{3}{2}$],k∈Z |
分析 三角函数的图象与直线y=b(0<b<A)的三个相邻交点的横坐标分别是1,2,4,至少提供两个方面的信息:
①第一个交点与第三个交点的差是一个周期;
②第一个交点与第二个交点的中点横坐标对应的函数值是最大值或最小值;
从这两个方面考虑求得参数ω,φ,从而利用三角函数的单调性求答案.
解答 解:与直线y=b(0<b<A)的三个相邻交点的横坐标分别是1,2,4,
知函数的周期为T=$\frac{2π}{ω}$=4-1=3,
解得ω=$\frac{2π}{3}$;
再由三角函数的图象与直线y=b(0<b<A)知:
1与2的中点必为函数的最大值的横坐标,
由五点法知$\frac{2π}{3}$×$\frac{3}{2}$+φ=$\frac{π}{2}$,
解得φ=-$\frac{π}{2}$;
∴f(x)=Asin($\frac{2π}{3}$x-$\frac{π}{2}$)=-Acos($\frac{2π}{3}$x),
令2kπ≤$\frac{2π}{3}$x≤2kπ+π,k∈Z,
解得3k≤x≤3k+$\frac{3}{2}$,k∈Z,
∴f(x)的单调递增区间是[3k,3k+$\frac{3}{2}$],(k∈Z).
故选:B.
点评 本题考查了三角函数的解析式以及三角函数的图象与性质的应用问题,是综合性题目.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源:2015-2016学年河南省商丘市高一文下学期期末考数学试卷(解析版) 题型:选择题
掷一枚均匀的硬币两次,事件M:一次正面朝上,一次反面朝上;事件N:至少一次正面朝上.下列结果正确的是( )
A.P(M)= ,P(N)=
,P(N)=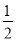
B.P(M)=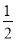 ,P(N)=
,P(N)=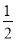
C.P(M)=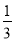 ,P(N)=
,P(N)=
D.P(M)=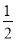 ,P(N)=
,P(N)=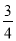
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{5}}{4}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com