
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 利用离心率的定义,分别求出f($\frac{2π}{3}$)、f($\frac{π}{3}$).即可求出f($\frac{2π}{3}$)-f($\frac{π}{3}$).
解答 解:由题意,M(c,$\frac{{b}^{2}}{a}$),θ=$\frac{2π}{3}$,tan$\frac{π}{3}$=$\frac{\frac{{b}^{2}}{a}}{a+c}$,∴e=$\sqrt{3}$+1,即f($\frac{2π}{3}$)=$\sqrt{3}$+1;
θ=$\frac{π}{3}$,tan$\frac{π}{6}$=$\frac{\frac{{b}^{2}}{a}}{a+c}$,∴e=$\frac{\sqrt{3}}{3}$+1,即f($\frac{π}{3}$)=$\frac{\sqrt{3}}{3}$+1,
∴f($\frac{2π}{3}$)-f($\frac{π}{3}$)=$\frac{2\sqrt{3}}{3}$,
故选A.
点评 本题考查离心率的定义,考查双曲线的性质,属于中档题.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源:2015-2016学年河南省商丘市高一理下学期期末考数学试卷(解析版) 题型:选择题
商丘一高某社团为了了解“早餐与健康的关系”,选取某班共有60名学生,现采用系统抽样的方法从中抽取6名学生做“早餐与健康”的调查,为此将学生编号为1,2,…,60.选取的这6名学生的编号可能是( )
A.1,2,3,4,5,6 B.6,16,26,36,46,56
C.1,2,4,8,16,32 D.3,9,13,27,36,54
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{5}}{4}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | -2016 | C. | 3024 | D. | -3024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1.4 | B. | 1.9 | C. | 2.2 | D. | 2.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
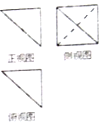 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积的最大值为2$\sqrt{3}$.
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积的最大值为2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com