
 根据下面的要求,求1+3+5+…+99的值.
根据下面的要求,求1+3+5+…+99的值.分析 (1)分析题目中的要求,发现这是一个累加型的问题,用循环结构来实现,在编写算法的过程中要注意,累加的初始值为0,累加值每一次增加2,退出循环的条件是i>100,把握住以上要点即可得解.
(2)根据流程图利用for语句可完成执行该问题的完整程序.
解答 解:(1)由题意,这是一个累加型的问题,用循环结构来实现,
由于累加的初始值为0,累加值每一次增加2,退出循环的条件是i>100,
故:①s=s+i;②i=i+2;③i≥100或i>99或(写一个即可)
(2)用for语句写出该算法如下:
s=0
For i=1 To 99 Step 2
s=s+i
Next
INPUT s
END
点评 本题考查了程序框图和伪代码.可利用循环语句来实现数值的累加(乘)常分如下步骤:①观察S的表达式分析,循环的初值、终值、步长②观察每次累加的值的通项公式③在循环前给累加器和循环变量赋初值,累加器的初值为0,累乘器的初值为1,环变量的初值同累加(乘)第一项的相关初值④在循环体中要先计算累加(乘)值,如果累加(乘)值比较简单可以省略此步,累加(乘),给循环变量加步长⑤输出累加(乘)值.属于基础题.


科目:高中数学 来源: 题型:选择题
| 不低于120分(优秀) | 低于120分(非优秀) | |
| 男 | 12 | 21 |
| 女 | 11 | 19 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超过0.01的前提下认为“该班学生英语成绩优秀与性别有关” | |
| B. | 在犯错误的概率不超过0.05的前提下认为“该班学生英语成绩优秀与性别有关” | |
| C. | 没有90%以上的把握认为“该班学生英语成绩优秀与性别有关” | |
| D. | 有90%以上的把握认为“该班学生英语成绩优秀与性别有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)、(2) | B. | (1)、(4) | C. | (3)、(4) | D. | (2)、(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$a 2 | B. | $\frac{\sqrt{3}}{4}$a 2 | C. | $\frac{\sqrt{6}}{2}$a 2 | D. | $\sqrt{6}$a 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y'=3sin2x' | B. | y'=3sin$\frac{x'}{2}$ | C. | y'=$\frac{1}{3}$sin2x' | D. | y'=$\frac{1}{3}sin\frac{x'}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
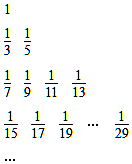 把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )| A. | $\frac{1}{99}$ | B. | $\frac{1}{87}$ | C. | $\frac{1}{81}$ | D. | $\frac{1}{85}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com