
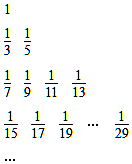 把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )| A. | $\frac{1}{99}$ | B. | $\frac{1}{87}$ | C. | $\frac{1}{81}$ | D. | $\frac{1}{85}$ |
 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 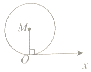 | B. | 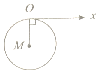 | C. | 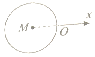 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X(万元) | 3 | 4 | 5 | 6 | 7 |
| Y(吨) | 90 | 83 | 75 | 65 | 52 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 数学成绩优秀(人) | 数学成绩不优秀(人) | 合计 | |
| 物理成绩优秀(人) | a=5 | b=2 | a+b=7 |
| 物理成绩不优秀(人) | c=1 | d=12 | c+d=13 |
| 合计 | a+c=6 | b+d=14 | n=a+b+c+d=20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个几何体的三视图如图所示,则该几何体的表面积为( )
一个几何体的三视图如图所示,则该几何体的表面积为( )| A. | 4π+8 | B. | $\frac{4π}{3}$+24 | C. | 4π+24 | D. | $\frac{4π}{3}$+8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{{\sqrt{7}}}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com