
| X(万元) | 3 | 4 | 5 | 6 | 7 |
| Y(吨) | 90 | 83 | 75 | 65 | 52 |
分析 (1)求出y关于x2的线性回归方程即可,
(2)求出利润Z关于x的函数,根据二次函数的性质可得利润Z最大.
解答 解:(1)令m=x2,则y与m具有线性相关关系,m与y的对于关系如下:
| m | 9 | 16 | 25 | 36 | 49 |
| y | 90 | 83 | 75 | 65 | 52 |
点评 本题考查了二次拟合的回归方程求解,数值预测,属于中档题.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:选择题
 如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的一个三棱锥的三视图,则该三棱锥的表面积为( )| A. | $\frac{{15+\sqrt{17}}}{2}$ | B. | $\frac{{13+\sqrt{17}}}{2}$ | C. | $\frac{{11+\sqrt{17}}}{2}$ | D. | $\frac{{9+\sqrt{17}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)、(2) | B. | (1)、(4) | C. | (3)、(4) | D. | (2)、(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$a 2 | B. | $\frac{\sqrt{3}}{4}$a 2 | C. | $\frac{\sqrt{6}}{2}$a 2 | D. | $\sqrt{6}$a 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
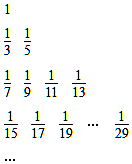 把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )| A. | $\frac{1}{99}$ | B. | $\frac{1}{87}$ | C. | $\frac{1}{81}$ | D. | $\frac{1}{85}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com