
| 数学成绩优秀(人) | 数学成绩不优秀(人) | 合计 | |
| 物理成绩优秀(人) | a=5 | b=2 | a+b=7 |
| 物理成绩不优秀(人) | c=1 | d=12 | c+d=13 |
| 合计 | a+c=6 | b+d=14 | n=a+b+c+d=20 |
分析 (1)由题意可知,即可求得a和d的值,即可求得a+c及b+d的值;
(2)由物理和数学成绩都优秀人数5人,则物理和数学成绩都优秀的概率;
(3)由观测值的计算公式算出随机变量K2的值,对照临界值表即可得到正确答案.
解答 解:(1)由b=2,a+b=7,则a=5,c=1,c+d=13,则d=12,
a+c=6,b+d=14,a+b+c+d=20,
∴2×2列联表:
| 数学成绩优秀(人) | 数学成绩不优秀(人) | 合计 | |
| 物理成绩优秀(人) | a=5 | b=2 | a+b=7 |
| 物理成绩不优秀(人) | c=1 | d=12 | c+d=13 |
| 合计 | a+c=6 | b+d=14 | n=a+b+c+d=20 |
点评 本题主要考查独立性检验的基本思想、方法及其简单应用和概率等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$a 2 | B. | $\frac{\sqrt{3}}{4}$a 2 | C. | $\frac{\sqrt{6}}{2}$a 2 | D. | $\sqrt{6}$a 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2$\sqrt{2}$,$\frac{3π}{4}$,$\frac{π}{6}$) | B. | (2$\sqrt{2}$,$\frac{π}{4}$,$\frac{π}{6}$) | C. | (2$\sqrt{2}$,$\frac{π}{4}$,$\frac{π}{3}$) | D. | (2$\sqrt{2}$,$\frac{3π}{4}$,$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
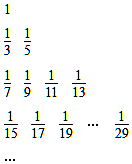 把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )
把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图,第k行有2k-1个数,第t行的第s个数(从左数起)记为A(t,s),则A(6,10)=( )| A. | $\frac{1}{99}$ | B. | $\frac{1}{87}$ | C. | $\frac{1}{81}$ | D. | $\frac{1}{85}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | { x丨0<x<1} | B. | { x丨0≤x<1} | C. | { x丨0<x≤1} | D. | { x丨-2<x≤1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com