
分析 (1)设等差数列{an}的首项为a1,公差为d,由题意可知$\left\{\begin{array}{l}{9{a}_{1}+36d=90}\\{15{a}_{1}+105d=240}\end{array}\right.$,解得即可,
(2)求出数列bn的通项公式,根据裂项求和求出Sn,即可求出t的范围.
解答 解:(1)设等差数列{an}的首项为a1,公差为d,
由S9=90,S15=240,
得$\left\{\begin{array}{l}{9{a}_{1}+36d=90}\\{15{a}_{1}+105d=240}\end{array}\right.$,
解得a1=d=2,
∴an=2+2(n-1)=2n,
Sn=2n+$\frac{n(n-1)×2}{2}$=n(n+1),
(2)∵anbn=$\frac{1}{(n+1)}$,
∴bn=$\frac{1}{2n(n+1)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+1}$),
∴Sn=$\frac{1}{2}$(1-$\frac{1}{2}$$+\frac{1}{2}$$-\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)=$\frac{1}{2}$(1-$\frac{1}{n+1}$)<$\frac{1}{2}$,
∴不等式Sn<t对于任意的n∈N*恒成立,
∴t≥$\frac{1}{2}$
点评 本题考查数列的通项公式和前n项和公式的求法,考查满足条件的实数的取值范围的求法,以及裂项求和,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 40 | C. | 60 | D. | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
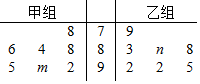 某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则m+n的值是( )
某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则m+n的值是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-1,3] | C. | (1,3) | D. | (1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在(0,$\frac{π}{4}}$)上单调递增,为奇函数 | B. | 周期为π,图象关于($\frac{π}{4},0}$)对称 | ||
| C. | 最大值为$\sqrt{2}$,图象关于直线x=$\frac{π}{2}$对称 | D. | 在(-$\frac{π}{2},0}$)上单调递增,为偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com