
分析 (1)由a=-1知,f(x)是确定的.对f(x)求导,由导函数的正负可以得到原函数的极值与单调区间.
(2)构造新的函数g(x),通过对g(x)求导,得到g(x)的单调区间,从而求出g(x)的最大值,进而得到要证明的问题.
解答 解:(1)当a=-1时,f(x)=-x-ln(-x)
f′(x)=-1-$\frac{1}{x}$
令f′(x)=0,得x=-1
-e≤x<-1时,f′(x)<0,f(x)单调递减
-1<x<0时,f′(x)>0,f(x)单调递增
∴f(x)单调递减区间是[-e,-1),单调递增区间是(-1,0)
f(x)有极小值,极小值是f(-1)=1.
(2)当a=-1时,由(1)知,f(x)的最小值为f(-1)=1
令g(x)=$\frac{1}{2}$-$\frac{ln(-x)}{x}$
∴g′(x)=-$\frac{1-ln(-x)}{{x}^{2}}$
当x∈[-e,0)时,g′(x)<0
∴g(x)在[-e,0)上单调递减
∴g(x)的最大值为g(-e)=$\frac{1}{2}$+$\frac{1}{e}$
∴f(x)min>g(x)max
∴当a=-1时,f(x)+$\frac{ln(-x)}{x}$>$\frac{1}{2}$恒成立.
点评 本题考查函数的单调性,极值问题.考查导数的应用.是中档题.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
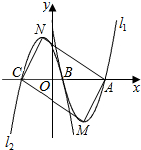 如图,己知抛物线11:y=x2-8x+12与x轴分别交于A、B两点,顶点为M.将抛物线11关于x轴作轴对称变换后再向左平移得到抛物线12,若抛物线12过点B,与x轴的另一个交点为C,顶点为N,则四边形AMCN的面积为32.
如图,己知抛物线11:y=x2-8x+12与x轴分别交于A、B两点,顶点为M.将抛物线11关于x轴作轴对称变换后再向左平移得到抛物线12,若抛物线12过点B,与x轴的另一个交点为C,顶点为N,则四边形AMCN的面积为32.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com