
 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(1,0)的动直线l与椭圆相交于A,B两点,当直线l平行于y轴时,直线l被椭圆C截得的线段长为2$\sqrt{2}$.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(1,0)的动直线l与椭圆相交于A,B两点,当直线l平行于y轴时,直线l被椭圆C截得的线段长为2$\sqrt{2}$.分析 (1)由已知得点$(1,\sqrt{2})$在椭圆C上,再由离心率性质列出方程组,求出a,b,从而求出椭圆的方程.
(2)设直线l的方程为x=my+1,与椭圆联立,得(m2+4)y2+2my-8=0,由此利用根的判别式、韦达定理、椭圆弦长公式能求出直线方程.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(1,0)的动直线l与椭圆相交于A,B两点,
当直线l平行于y轴时,直线l被椭圆C截得的线段长为2$\sqrt{2}$.
∴点$(1,\sqrt{2})$在椭圆C上.
∴$\left\{\begin{array}{l}\frac{1}{a^2}+\frac{2}{b^2}=1\\{a^2}-{b^2}={c^2}\\ \frac{c}{a}=\frac{{\sqrt{3}}}{2}\end{array}\right.$,解得$a=3,b=\frac{3}{2}$.…(4分)
∴椭圆的方程为$\frac{x^2}{9}+\frac{{4{y^2}}}{9}=1$.…(5分)
(2)当直线l与x轴平行时,△ABD不存在,…(6分)
∴设直线l的方程为x=my+1,并设两点A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}\frac{x^2}{9}+\frac{{4{y^2}}}{9}=1\\ x=my+1\end{array}\right.$,得(m2+4)y2+2my-8=0,
其判别式△=4m2+32(m2+4)=36m2+128>0,…(8分)
∴${y_1}+{y_2}=-\frac{2m}{{{m^2}+4}},{y_1}{y_2}=-\frac{8}{{{m^2}+4}}$,
∴${S_{△ABD}}=\frac{1}{2}|DP||{y_1}-{y_2}|=2\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}$
=$2\sqrt{{{(\frac{2m}{{{m^2}+4}})}^2}+\frac{32}{{{m^2}+4}}}=\frac{4}{{{m^2}+4}}\sqrt{9{m^2}+32}$…(10分)
假设存在直线l,则有,$\frac{4}{{{m^2}+4}}\sqrt{9{m^2}+32}=\frac{10}{3}\sqrt{2}$,
解得m2=2,负解删除,∴$m=±\sqrt{2}$,…(12分)
故存在直线l方程为$x=±\sqrt{2}y+1$,使得${S_{△ABD}}=\frac{{10\sqrt{2}}}{3}$.…(13分)
点评 本题考查椭圆方程、直线方程的求法,是中档题,解题时要认真审题,注意椭圆性质、根的判别式、韦达定理、椭圆弦长公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
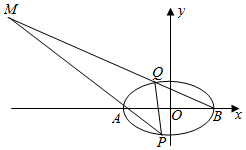 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{3}$,且椭圆的四个顶点相连得到的凸四边形的面积为12$\sqrt{2}$.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{3}$,且椭圆的四个顶点相连得到的凸四边形的面积为12$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
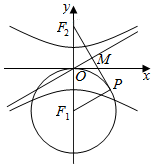 如图,已知F1,F2是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的下,上焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为( )
如图,已知F1,F2是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的下,上焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为( )| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com