Question

如图，海上有两个小岛相距10，船O将保持观望A岛和B岛所成的视角为，现从船O上派下一只小艇沿方向驶至处进行作业，且．设。

（1）用分别表示和，并求出的取值范围；
（2）晚上小艇在处发出一道强烈的光线照射A岛，B岛至光线的距离为，求BD的最大值．

Answer 1

（1）；，（2）10

解析试题分析：（1）在和中，分别用余弦定理AC，AB，然后两式相加即得的表达式；两式相减即得的表达式，由和确定x的取值范围.（2）由、和可得到关于BD的函数式，然后通过求导，求出BD的最大值.
试题解析：解：（1）在中，，，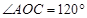
由余弦定理得，，
又，
所以 ①，       1分
在中，，
由余弦定理得，
 ②，       3分
①+②得，
①②得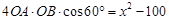，即，          4分
又，所以，即，
又，即， 所以                  6分
（2）易知，
故，                   8分
又，设，
所以，                              9分
又                                                10分
则在上是增函数，
所以的最大值为，即BD的最大值为10．                 12分
（利用单调性定义证明在上是增函数，同样给满分；如果直接说出上是增函数，但未给出证明，扣2分．）
考点：1.余弦定理；2.函数的导数及其导数性质的应用.