
【题目】在某批次的某种灯泡中,随机地抽取![]() 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于![]() 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于![]() 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
寿命(天) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)根据频率分布表中的数据,写出![]() 、
、![]() 的值;
的值;
(2)某人从灯泡样品中随机地购买了![]() 个,如果这
个,如果这![]() 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求![]() 的最小值;
的最小值;
(3)某人从这个批次的灯泡中随机地购买了![]() 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用![]() 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)分布列见解析,
;(3)分布列见解析,![]() .
.
【解析】
(1)根据频数、频率和样本容量之间的关系可得出![]() 、
、![]() 的值;
的值;
(2)由频率分布表知按分层抽样法,购买灯泡数![]() 个,由此能求出
个,由此能求出![]() 的最小值;
的最小值;
(3)![]() 的所有取值为
的所有取值为![]() 、
、![]() 、
、![]() 、
、![]() ,分别求出相对应的概率,由此能求出
,分别求出相对应的概率,由此能求出![]() 的分布列和数学期望.
的分布列和数学期望.
(1)由题意可得![]() ,
,![]() ;
;
(2)由表可知:灯泡样品中优等品有![]() 个,正品有
个,正品有![]() 个,次品有
个,次品有![]() 个,
个,
![]() 优等品、正品和次品的比例为
优等品、正品和次品的比例为![]() ,
,
![]() 按分层抽样法,购买灯泡数为
按分层抽样法,购买灯泡数为![]() 个,
个,
因此,![]() 的最小值为
的最小值为![]() ;
;
(3)![]() 的所有取值为
的所有取值为![]() 、
、![]() 、
、![]() 、
、![]() ,
,
由题意,购买一个灯泡,且这个灯泡是次品的概率为![]() ,
,
从本批次灯泡中购买![]() 个,可看成
个,可看成![]() 次独立重复试验,则
次独立重复试验,则![]() .
.
![]() ,
,![]() ,
,
![]() ,
, .
.
所以,随机变量![]() 的分布列如下表所示:
的分布列如下表所示:
|
|
|
|
|
|
|
|
|
|
因此,随机变量![]() 的数学期望为
的数学期望为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程是 (φ为参数,a>0),直线l的参数方程是
(φ为参数,a>0),直线l的参数方程是![]() (t为参数),曲线C与直线l有一个公共点在x轴上,以坐标原点为极点,x轴的正半轴为极轴建立坐标系.
(t为参数),曲线C与直线l有一个公共点在x轴上,以坐标原点为极点,x轴的正半轴为极轴建立坐标系.
(1)求曲线C的普通方程;
(2)若点A(ρ1,θ),B(ρ2,θ+![]() ),C(ρ3,θ+
),C(ρ3,θ+![]() )在曲线C上,求
)在曲线C上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列的定义为:在一个数列中,从第二项起,如果每一项与它的前一项的差都为同一个常数,那么这个数叫做等差数列,这个常数叫做该数列的公差.类比等差数列的定义给出“等和数列”的定义:_____________________________________;已知数列![]() 是等和数列,且
是等和数列,且![]() ,公和为
,公和为![]() ,那么
,那么![]() 的值为____________.这个数列的前
的值为____________.这个数列的前![]() 项和
项和![]() 的计算公式为_____________________________________.
的计算公式为_____________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
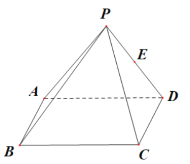
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() ,侧面
,侧面![]() 为等边三角形且垂直于底面
为等边三角形且垂直于底面![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)在棱![]() 上取一点
上取一点![]() 使直线
使直线![]() ∥平面
∥平面![]() 并证明;
并证明;
(2)在(1)的条件下,当棱![]() 上存在一点
上存在一点![]() ,使得直线
,使得直线![]() 与底面
与底面![]() 所成角为
所成角为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() :
:![]() ,
,![]() ,
,![]() ,…,
,…,![]() 为1,2,3,…,
为1,2,3,…,![]() 的一个排列,若
的一个排列,若![]() 互不相同,则称数列
互不相同,则称数列![]() 具有性质
具有性质![]() .
.
(1)若![]() ,且
,且![]() ,写出具有性质
,写出具有性质![]() 的所有数列
的所有数列![]() ;
;
(2)若数列![]() 具有性质
具有性质![]() ,证明:
,证明:![]() ;
;
(3)当![]() 时,分别判断是否存在具有性质
时,分别判断是否存在具有性质![]() 的数列
的数列![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共1000名男生中随机抽取50人测量身高,据测量,被测学生身高全部介于![]() 到
到![]() 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() .如图是按上述分组方法得到的频率分布直方图的一部分.其中第六组、第七组、第八组人数依次构成等差数列.
.如图是按上述分组方法得到的频率分布直方图的一部分.其中第六组、第七组、第八组人数依次构成等差数列.
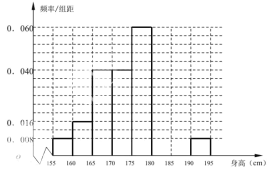
(1)求第六组、第七组的频率,并估计高三年级全体男生身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(2)学校决定让这五十人在运动会上组成一个高旗队,在这五十人中要选身高在![]() 以上(含
以上(含![]() )的两人作为队长,求这两人在同一组的概率.
)的两人作为队长,求这两人在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了解本市1万名小学生的普通话水平,在全市范围内进行了普通话测试,测试后对每个小学生的普通话测试成绩进行统计,发现总体(这1万名小学生普通话测试成绩)服从正态分布![]() .
.
(1)从这1万名小学生中任意抽取1名小学生,求这名小学生的普通话测试成绩在![]() 内的概率;
内的概率;
(2)现在从总体中随机抽取12名小学生的普通话测试成绩,对应的数据如下:50,52,56,62,63,68,65,64,72,80,67,90.从这12个数据中随机选取4个,记![]() 表示大于总体平均分的个数,求
表示大于总体平均分的个数,求![]() 的方差.
的方差.
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com