
【题目】如图所示,四棱锥P﹣ABCD的底面是边长为2的正方形,平面PAD⊥平面ABCD,PA⊥AD,∠PDA=45°,E,F分别为AB,PC的中点.
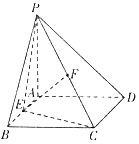
(1)证明:EF∥平面PAD;
(2)在线段BC上是否存在一点H,使平面PAH⊥平面DEF?若存在,求此时二面角C﹣HD﹣P的平面角的正切值:若不存在,说明理由.
【答案】(1)证明见解析(2)存在,正切值为![]()
【解析】
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 是
是![]() 的中位线,推导出
的中位线,推导出![]() 是平行四边形,从而
是平行四边形,从而![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;
;
(2)当![]() 为
为![]() 中点时,
中点时,![]() ,推导出
,推导出![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角的补角,由此能求出二面角
的平面角的补角,由此能求出二面角![]() 的平面角的正切值.
的平面角的正切值.
(1)证明:取PD中点M,连结AM,FM,

则MF是△PCD的中位线,
∴MF∥CD,且MF![]() ,
,
又四边形ABCD是正方形,则AE∥CD,
且E为AB中点,则AE![]() AB
AB![]() CD,
CD,
∴AE∥MF,且AE=MF,∴AMFE是平行四边形,
∴EF∥AM,
又AM![]() 平面PAD,EF
平面PAD,EF![]() 平面PAD,
平面PAD,
∴EF∥平面PAD.
(2)解:在正方形![]() 中,取H为BC中点,
中,取H为BC中点,![]() 为
为![]() 的中点,易证ED⊥AH,
的中点,易证ED⊥AH,
又∵AP⊥ED,且AP,AH为平面APH内两相交直线,
∴ED⊥平面PAH,
又ED![]() 平面DEF,∴平面EFD⊥平面PAH,
平面DEF,∴平面EFD⊥平面PAH,
此时,过点A作AG⊥DH于点G,

则∠PGA为二面角C﹣HD﹣P的平面角的补角,
由![]() ,则AG
,则AG![]() ,tan∠AGP
,tan∠AGP![]() ,
,
∴二面角C﹣HD﹣P的平面角的正切值为![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,下列命题:
,下列命题:
①![]() 的定义域为
的定义域为![]() ;
;
②![]() 是奇函数;
是奇函数;
③![]() 在
在![]() 上单调递增;
上单调递增;
④若实数![]() 满足
满足![]() ,则
,则![]() ;
;
⑤设函数![]() 在上的最大值为
在上的最大值为![]() ,最小值为
,最小值为![]() ,则
,则![]() .
.
其中真命题的序号是______.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+2φ)为偶函数,其中φ∈(0,![]() ),则下列关于函数g(x)=sin(2x+φ)的描述正确的是( )
),则下列关于函数g(x)=sin(2x+φ)的描述正确的是( )
A.g(x)在区间[![]() ]上的最小值为﹣1
]上的最小值为﹣1
B.g(x)的图象可由函数f(x)的图象向上平移一个单位,再向右平移![]() 个单位长度得到
个单位长度得到
C.g(x)的图象的一个对称中心为(![]() ,0)
,0)
D.g(x)的一个单调递增区间为[0,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设递增等比数列{an}的前n项和为Sn,且a2=3,S3=13,数列{bn}满足b1=a1,点P(bn,bn+1)在直线x﹣y+2=0上,n∈N*.
(1)求数列{an},{bn}的通项公式;
(2)设cn![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着新政策的实施,海淘免税时代于2016年4月8日正式结束,新政策实施后,海外购物的费用可能会增加.为了解新制度对海淘的影响,某网站调查了喜欢海淘的1000名网友,其态度共有两类:第一类是会降低海淘数量,共有400人,第二类是不会降低海淘数量,共有600人,若从这1000人中按照分层抽样的方法抽取10人后进行打分,其打分的茎叶图如下图所示,图中有数据缺失,但已知“第一类”和“第二类”网民打分的均值相等,则“第一类”网民打分的方差为( )
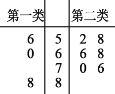
A.159B.179C.189D.209
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的图象为C,下面结论正确的是( )
的图象为C,下面结论正确的是( )
A.函数f(x)的最小正周期是2π.
B.函数f(x)在区间![]() 上是递增的
上是递增的
C.图象C关于点![]() 对称
对称
D.图象C由函数g(x)=sin2x的图象向左平移![]() 个单位得到
个单位得到
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com