
| A-B |
| 2 |
| C |
| 2 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-2
|
| 1 |
| 4 |
| A-B |
| 2 |
| C |
| 2 |
| 1+cos(A-B) |
| 2 |
| 1+cosC |
| 2 |
| 1 |
| 4 |
| tanAtanB |
| tanA+tanB |
| 1-tanAtanB |
| 1 | ||
1-
|
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、“正四棱锥的底面是正方形”的逆命题为真命题. | ||
| B、“ac2>bc2”的充要条件是“a>b”. | ||
C、不等式
| ||
| D、若“p或q”是真命题,则p,q中至少有一个真命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:
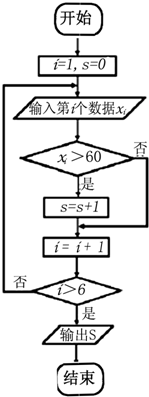 某学生一个学期的数学测试成绩一共记录了6个数据:x1=52,x2=70,x3=68,x4=55,x5=85,x6=90,执行如图所示的程序框图,那么输出的S是( )
某学生一个学期的数学测试成绩一共记录了6个数据:x1=52,x2=70,x3=68,x4=55,x5=85,x6=90,执行如图所示的程序框图,那么输出的S是( )| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
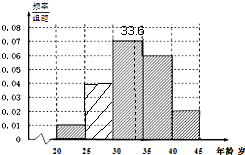 某市要对两千多名出租车司机的年龄进行调查,现从的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )
某市要对两千多名出租车司机的年龄进行调查,现从的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )| A、31.6岁 |
| B、32.6岁 |
| C、33.6岁 |
| D、36.6岁 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com