
分析 (Ⅰ)代入a值,求出导函数,找出极值点,得出函数的单调区间即可;
(Ⅱ)由题意即$f{(x)_{min}}<\frac{a}{2}$,当a>0时,f(x)min=f(1),当a<0,$f(1)>\frac{a}{2}$恒成立,由此利用导数性质能求出参数a的取值范围.
解答 解:(Ⅰ)$f(x)=x{e^x}-\frac{x^2}{2}-x+1$,
f'(x)=ex+xex-x-1=(ex-1)(x+1)=0时x1=0,x2=-1
| x | (-∞,-1) | -1 | (-1,0) | 0 | (0,+∞) |
| f'(x) | + | - | + | ||
| f(x) | 增 | 减 | 增 |
| x | (-∞,0) | 0 | $({0,-\frac{1}{a}})$ | $-\frac{1}{a}$ | $({-\frac{1}{a},+∞})$ |
| g'(x) | + | - | + | ||
| g(x) | ↑ | ↓ | ↑ |
点评 本题考查导数及其应用、不等式、函数等基础知识,考查考查推理论证能力、运算求解能力、抽象概括能力,考查化归与转化思想、函数与方程思想、分类与整合思想,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
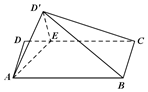 如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$,1) | B. | (-∞,$\frac{1}{3}$)∪(1,+∞) | C. | (-$\frac{1}{3}$,1) | D. | D、(-∞,$-\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (0,3) | C. | (-∞,0)∪(3,+∞) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{7}{2}$ | C. | 3 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
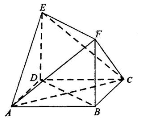 在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.
在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com