
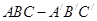 ,
,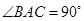 ,
,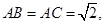 AA′=1,点M,N分别为
AA′=1,点M,N分别为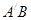 和
和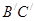 的中点。
的中点。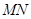 ∥平面
∥平面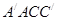 ;
;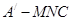 的体积。(锥体体积公式V=
的体积。(锥体体积公式V=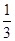 Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高)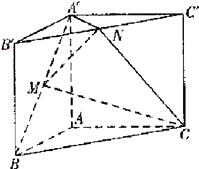
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 表示两条直线,
表示两条直线, 表示两个平面,现给出下列命题:
表示两个平面,现给出下列命题: ,则
,则 ; ② 若
; ② 若 ,则
,则 ;
; ,则
,则 ; ④ 若
; ④ 若 ,则
,则 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
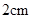 的圆柱器皿中(底面水平放置),量得水面的高度为
的圆柱器皿中(底面水平放置),量得水面的高度为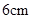 .若将这些水倒入轴截面是正三角形的倒置的圆锥形器皿中,则水面的高度是( )
.若将这些水倒入轴截面是正三角形的倒置的圆锥形器皿中,则水面的高度是( )A.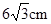 | B.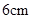 | C.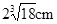 | D.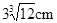 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
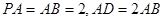 ,PA
,PA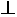 平面ABCD, E,F分别是BC,PC的中点。
平面ABCD, E,F分别是BC,PC的中点。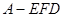 的体积。
的体积。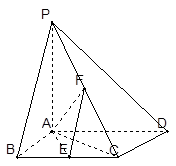
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
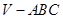 中,
中,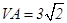 ,
,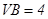 ,
,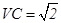 ,点
,点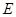 为侧棱
为侧棱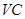 上的一点,
上的一点,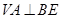 ,且顶点
,且顶点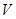 在底面
在底面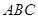 上的射影为底面的垂心.如果球
上的射影为底面的垂心.如果球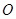 是三棱锥
是三棱锥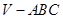 的外接球,则
的外接球,则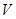 ,
, 两点的球面距离是( )
两点的球面距离是( )A.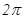 | B.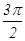 | C.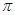 | D.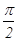 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com