
分析 利用正弦定理可知a,b,c成公比数列,公比为q.于是b=aq,c=aq2,根据三角形两边之和大于第三边列出不等式组解出q的范围.
解答 解:∵sinA、sinB、sinC成公比为q的等比数列,
∴q=$\frac{sinB}{sinA}=\frac{sinC}{sinB}$,∴q=$\frac{b}{a}=\frac{c}{b}$.
∴b=aq,c=aq2.
由两边之和大于第三边得:$\left\{\begin{array}{l}{a+aq>a{q}^{2}}\\{a+a{q}^{2}>aq}\\{aq+a{q}^{2}>a}\end{array}\right.$,
∴$\left\{\begin{array}{l}{1+q>{q}^{2}}\\{1+{q}^{2}>q}\\{q+{q}^{2}>1}\end{array}\right.$,解得:$\frac{\sqrt{5}-1}{2}$<q<$\frac{\sqrt{5}+1}{2}$.
故答案为($\frac{\sqrt{5}-1}{2}$,$\frac{\sqrt{5}+1}{2}$).
点评 本题考查了正弦定理,不等式的解法,属于中档题.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:选择题
| A. | 46m3 | B. | 44m3 | C. | 26m3 | D. | 25m3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
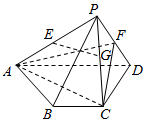 如图.四棱锥P-ABCD中,底面ABCD为等腰梯形,BC∥AD,平面PCD⊥平面ABCD,E.F,G分别是PA,PD,PC的中点,PF⊥PG,AB=BC=CD=$\frac{1}{2}$AD.
如图.四棱锥P-ABCD中,底面ABCD为等腰梯形,BC∥AD,平面PCD⊥平面ABCD,E.F,G分别是PA,PD,PC的中点,PF⊥PG,AB=BC=CD=$\frac{1}{2}$AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 63 | B. | 93 | C. | 126 | D. | 1023 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com