
| AЃЎ | -$\frac{1}{2}$ | BЃЎ | -$\frac{2}{3}$ | CЃЎ | -$\frac{1}{3}$ | DЃЎ | -$\frac{1}{4}$ |
ЗжЮі ИљОнШ§ИіЪ§ГЩЕШБШЪ§СаЕУЕНcos2ІШЕФжЕЃЌ
дйИљОн|$\overrightarrow{a}$|Ён1ЃЌ|$\overrightarrow{b}$|Ён3КЭЖўБЖНЧЙЋЪНЧѓГіcos2ІШЕФзюДѓжЕЃЎ
НтД№ НтЃКЯђСП$\overrightarrow{a}$ЃЌ$\overrightarrow{b}$ЕФМаНЧЮЊІШЃЌ|$\overrightarrow{a}$|Ён1ЃЌ|$\overrightarrow{b}$|Ён3ЃЌЧв|$\overrightarrow{a}$|ЃЌ$\overrightarrow{a}$•$\overrightarrow{b}$ЃЌ|$\overrightarrow{b}$|ГЩЕШБШЪ§СаЃЌ
Ёр|$\overrightarrow{a}$|ЁС|$\overrightarrow{b}$|=ЃЈ$\overrightarrow{a}$•$\overrightarrow{b}$ЃЉ2ЃЌ
Ёрcos2ІШ=$\frac{1}{|\overrightarrow{a}|ЁС|\overrightarrow{b}|}$Ём$\frac{1}{3}$ЃЌ
МД$\frac{1+cos2ІШ}{2}$Ём$\frac{1}{3}$ЃЌ
Ёрcos2ІШЁм-$\frac{1}{3}$ЃЌ
дђcos2ІШЕФзюДѓжЕЮЊ-$\frac{1}{3}$ЃЎ
ЙЪбЁЃКCЃЎ
ЕуЦР БОЬтПМВщСЫЦНУцЯђСПЕФЪ§СПЛ§вдМАБЖНЧЙЋЪНЕФдЫгУЮЪЬтЃЌЪЧЛљДЁЬтЃЎ


 гІгУЬтзївЕБОЯЕСаД№АИ
гІгУЬтзївЕБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 2 | BЃЎ | 4 | CЃЎ | 3$\sqrt{2}$ | DЃЎ | 2+$\sqrt{2}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
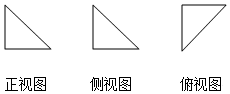 вбжЊвЛИіМИКЮЬхЕФе§ЪгЭМЁЂВрЪгЭМЁЂИЉЪгЭМЖМЪЧбќГЄЮЊ1ЕФЕШбќжБНЧШ§НЧаЮЃЈШчЭМЫљЪОЃЉЃЌдђИУМИКЮЬхЕФЬхЛ§ЪЧЃЈЁЁЁЁЃЉ
вбжЊвЛИіМИКЮЬхЕФе§ЪгЭМЁЂВрЪгЭМЁЂИЉЪгЭМЖМЪЧбќГЄЮЊ1ЕФЕШбќжБНЧШ§НЧаЮЃЈШчЭМЫљЪОЃЉЃЌдђИУМИКЮЬхЕФЬхЛ§ЪЧЃЈЁЁЁЁЃЉ| AЃЎ | 1 | BЃЎ | $\frac{1}{2}$ | CЃЎ | $\frac{1}{3}$ | DЃЎ | $\frac{1}{6}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com