
分析 由题意可得△ABC、△ACD都是等边三角形,AP∈[0,1],再利用两个向量的加减法及其几何意义求得$\overrightarrow{PB}$•$\overrightarrow{PD}$=${(AP-\frac{1}{2})}^{2}$-$\frac{3}{4}$,再利用二次函数的性质求得$\overrightarrow{PB}$•$\overrightarrow{PD}$的最大值.
解答 解:由题意可得△ABC、△ACD都是等边三角形,∠PAB=∠PAD=$\frac{π}{3}$,AP∈[0,1],
则$\overrightarrow{PB}$•$\overrightarrow{PD}$=($\overrightarrow{AB}$-$\overrightarrow{AP}$)•($\overrightarrow{AD}$-$\overrightarrow{AP}$)=${\overrightarrow{AP}}^{2}$-$\overrightarrow{AP}$($\overrightarrow{AB}$+$\overrightarrow{AD}$)+$\overrightarrow{AB}•\overrightarrow{AD}$=${\overrightarrow{AP}}^{2}$-$\overrightarrow{AP}•\overrightarrow{AC}$+1×1cos∠BAD
=AP2-AP-$\frac{1}{2}$=${(AP-\frac{1}{2})}^{2}$-$\frac{3}{4}$,
故当AP=0或AP=1时,$\overrightarrow{PB}$•$\overrightarrow{PD}$的最大值为-$\frac{1}{2}$,
故答案为:$-\frac{1}{2}$.
点评 本题主要考查两个向量的加减法及其几何意义,两个向量的数量积的定义,二次函数的性质,属于基础题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
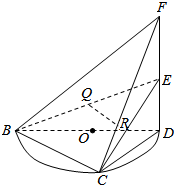 如图:$\widehat{BCD}$是直径为$2\sqrt{2}$的半圆,O为圆心,C是$\widehat{BD}$上一点,且$\widehat{BC}=2\widehat{CD}$.DF⊥CD,且DF=2,$BF=2\sqrt{3}$,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.
如图:$\widehat{BCD}$是直径为$2\sqrt{2}$的半圆,O为圆心,C是$\widehat{BD}$上一点,且$\widehat{BC}=2\widehat{CD}$.DF⊥CD,且DF=2,$BF=2\sqrt{3}$,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com