
分析 利用公式12+22+32+…+n2=$\frac{n(n+1)(2n+1)}{6}$和等比数列的求和公式进行猜想,再用数学归纳法证明.
解答 解:1×4+2×5+3×6+…+n(n+3)=$\frac{n(n+1)(n+5)}{3}$.
证明:当n=1时,1×4=4,$\frac{1×2×6}{3}$=4,显然结论成立;
假设n=k时,结论成立,即1×4+2×5+3×6+…+k(k+3)=$\frac{k(k+1)(k+5)}{3}$,
则n=k+1时,1×4+2×5+3×6+…+k(k+3)+(k+1)(k+4)=$\frac{k(k+1)(k+5)}{3}$+(k+1)(k+4)
=(k+1)($\frac{k(k+5)}{3}$+k+4)=$\frac{(k+1)({k}^{2}+8k+12)}{3}$
=$\frac{(k+1)(k+2)(k+6)}{3}$.
∴当n=k+1时,结论成立.
综上,1×4+2×5+3×6+…+n(n+3)=$\frac{n(n+1)(n+5)}{3}$.
点评 本题考查了数学归纳法,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是平行四边形或梯形 | B. | 是梯形 | ||
| C. | 不是平行四边形,也不是梯形 | D. | 是平行四边形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
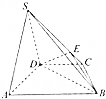 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,AB∥DC,△SAD是等边三角形,且SD=2,BD=2$\sqrt{3}$,AB=2CD=4.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,AB∥DC,△SAD是等边三角形,且SD=2,BD=2$\sqrt{3}$,AB=2CD=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB上的点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
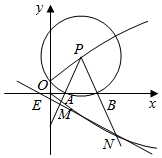 已知点F是抛物线C:y2=4x的焦点,P是抛物线C在第一象限内的点,且|PF|=5.
已知点F是抛物线C:y2=4x的焦点,P是抛物线C在第一象限内的点,且|PF|=5.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=-8 b=-10 | B. | a=-4 b=-9 | C. | a=-1 b=9 | D. | a=-1 b=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com