某初级中学有学生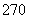
人，其中一年级
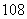人，二、三年级各
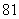人，现要利用抽样方法取
人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案，使用简单随机抽样和分层抽样时，将学生按一、二、三年级依次统一编号为
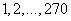；使用系统抽样时，将学生统一随机编号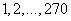，并将整个编号依次分为段.如果抽得号码有下列四种情况：
①7，34，61，88，115， 142，169，196，223，250；
②5，9，100，107，111，121，180，195，200，265；
③11，38，65，92，119，146，173，200，227，254；
④30，57，84，111，138，165，192，219，246，270；
关于上述样本的下列结论中，正确的是（ ）
A．②、③都不能为系统抽样 B．②、④都不能为分层抽样
C．①、④都可能为系统抽样 D．①、③都可能为分层抽样
科目：高中数学 来源： 题型：
设满足以下两个条件的有穷数列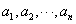
为n（n=2,3,4,…,）阶“期待数列”：
①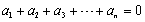 
；
②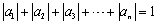 
.
（Ⅰ）分别写出一个单调递增的3阶和4阶“期待数列”；
（Ⅱ）若某2k+1(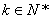
)阶“期待数列”是等差数列，求该数列的通项公式；
（Ⅲ）记n阶“期待数列”的前k项和为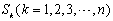
，
试证：（1）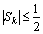
； （2）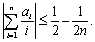
查看答案和解析>>
科目：高中数学 来源： 题型：
在直角坐标系
中，曲线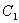
的参数方程为
，（
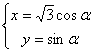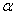为参数），以原点
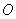为极点，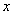
轴正半轴为极轴，建立极坐标系，曲线
的极坐标方程为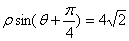
.
(1) 求曲线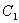的普通方程与曲线的直角坐标方程；
(2) 设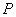
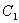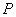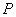为曲线上的动点，求点到上点的距离的最小值，并求此时点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
从装有2个红球和2个黑球的口袋内任取2个球，那么互斥 而不对立的两个事件是( )
A.“至少有一个黑球”与“都是黑球”
B.“至少有一个黑球”与“都是红球”
C.“至少有一个黑球”与“至少有一个红球”
D.“恰有一个黑球”与“恰有两个黑球”
查看答案和解析>>
科目：高中数学 来源： 题型：
参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏，但可见部分信息如下，据此解答如下问题：
（Ⅰ）求参加数学抽测的人数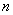
、抽测成绩的中位数及分数分别在
，
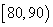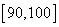内的人数；
（Ⅱ）若从分数在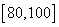
内的学生中任选两人进行调研谈话，求恰好有一人分数在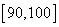内的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的值为7,则输出
的值是( ) 
C．22 D．17
在区间[0，2]上有两个零点，则实数
的取值范围是________ . 
，
，则
B．
C．
D．
满足约束条件
，则
的最大值是 ．