
【题目】若函数f(x)=3sin(2x﹣ ![]() )的图象为C,则下列结论中正确的序号是 . ①图象C关于直线x=
)的图象为C,则下列结论中正确的序号是 . ①图象C关于直线x= ![]() 对称;
对称;
②图象C关于点( ![]() ,0)对称;
,0)对称;
③函数f(x)在区间(﹣ ![]() ,
, ![]() )内不是单调的函数;
)内不是单调的函数;
④由y=3sin2x的图象向右平移 ![]() 个单位长度可以得到图象C.
个单位长度可以得到图象C.
【答案】①②
【解析】解:因为当x= ![]() 时,f(x)=3sin(2×
时,f(x)=3sin(2× ![]() ﹣
﹣ ![]() )=3sin
)=3sin ![]() , 所以直线x=
, 所以直线x= ![]() 是图象的对称轴,故①正确;
是图象的对称轴,故①正确;
因为当x= ![]() 时,f(x)=3sin(2×
时,f(x)=3sin(2× ![]() ﹣
﹣ ![]() )=0,
)=0,
所以函数图象关于点( ![]() ,0)对称,故②正确;
,0)对称,故②正确;
令﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤
≤ ![]() ,解得x∈[﹣
,解得x∈[﹣ ![]() ,
, ![]() ],
],
所以函数的一个增区间是[﹣ ![]() ,
, ![]() ],因此f(x)在区间[0,
],因此f(x)在区间[0, ![]() ]上是增函数,故③不正确;
]上是增函数,故③不正确;
由y=3sin2x的图象向右平移 ![]() 个单位,得到的图象对应的函数表达式为
个单位,得到的图象对应的函数表达式为
y=3sin2(x﹣ ![]() )=3sin(2x﹣
)=3sin(2x﹣ ![]() ),所以所得图象不是函数f(x)=3sin(2x﹣
),所以所得图象不是函数f(x)=3sin(2x﹣ ![]() )的图象C,故④不正确
)的图象C,故④不正确
所以答案是:①②.
【考点精析】关于本题考查的函数y=Asin(ωx+φ)的图象变换,需要了解图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能得出正确答案.
的图象才能得出正确答案.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】不等式x2﹣4x>2ax+a对一切实数x都成立,则实数a的取值范围是( )
A.(1,4)
B.(﹣4,﹣1)
C.(﹣∞,﹣4)∪(﹣1,+∞)
D.(﹣∞,1)∪(4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB. (Ⅰ)证明:A=2B
(Ⅱ)若△ABC的面积S= ![]() ,求角A的大小.
,求角A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
回归方程为 ![]() =bx+a,其中b=
=bx+a,其中b= 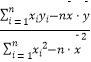 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,求出y与x的回归方程 ![]() =bx+a;
=bx+a;
(3)预测销售额为115万元时,大约需要多少万元广告费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( ) 
A.2,5
B.2,4
C.0,4
D.0,5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面内到定点F(0,1)和定直线l:y=﹣1的距离之和等于4的动点的轨迹为曲线C,关于曲线C的几何性质,给出下列四个结论: ①曲线C的方程为x2=4y;
②曲线C关于y轴对称
③若点P(x,y)在曲线C上,则|y|≤2;
④若点P在曲线C上,则1≤|PF|≤4
其中,所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=5,a2=2,an=2an﹣1+3an﹣2 , (n≥3) (Ⅰ)证明数列{an﹣3an﹣1}成等比数列,并求数{an}列的通项公式an;
(Ⅱ)若数列bn= ![]() (an+1+an),求数列{bn}的前n项和Sn .
(an+1+an),求数列{bn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com