
| A. | 偶函数且它的图象关于点 (π,0)对称 | |
| B. | 奇函数且它的图象关于点 (π,0)对称 | |
| C. | 奇函数且它的图象关于点($\frac{3π}{2}$,0)对称 | |
| D. | 偶函数且它的图象关于点($\frac{3π}{2}$,0)对称 |
分析 根据题意可得g(x)=f($\frac{3π}{4}$-x)=f(x-$\frac{π}{4}$),故g(x)可以看成把f(x)的图象向右平移$\frac{π}{4}$个单位得到的,再根据对称轴和对称中心最少相差$\frac{1}{4}$T,得出结论.
解答 解:∵函数 f(x)=asinx-bcosx (a,b为常数,a≠0,x∈R)在x=$\frac{π}{4}$处取得最小值,最小正周期为2π,
则f($\frac{3π}{4}$-x)=f(x-$\frac{π}{4}$),则函数g(x)=f($\frac{3π}{4}$-x)=f(x-$\frac{π}{4}$).
故g(x)可以看成把f(x)的图象向右平移$\frac{π}{4}$个单位得到的,即x=$\frac{π}{2}$是g(x)的图象的一个对称轴.
由于g($\frac{π}{2}$)=f($\frac{π}{4}$)对应g(x)的最小值,而对称轴和对称中心最少相差$\frac{1}{4}$T=$\frac{π}{2}$,故(0,0)和(π,0)是g(x)的对称中心,
故选:B.
点评 本题主要考查三角函数的图象的对称性,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | (2,8) | B. | (-2,-8) | C. | (1,1)或(-1,-1) | D. | $(-\frac{1}{2},-\frac{1}{8})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<ef(0),f(2)<e2f(0) | B. | f(1)>ef(0),f(2)<e2f(0) | C. | f(1)<ef(0),f(2)>e2f(0) | D. | f(1)>ef(0),f(2)>e2f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 重心(三条中线交点) | B. | 内心(三条角平分线交点) | ||
| C. | 垂心(三条高线交点) | D. | 外心(三边中垂线交点) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
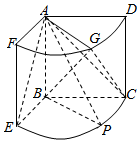 如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.
如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,海平面某区域内有A,B,C三座小岛,岛C在A的北偏东70°方向,岛C在B的北偏东40°方向,且A,B两岛间的距离为3海里.
如图,海平面某区域内有A,B,C三座小岛,岛C在A的北偏东70°方向,岛C在B的北偏东40°方向,且A,B两岛间的距离为3海里.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | a<f'(1)<f'(2) | B. | f'(1)<a<f'(2) | C. | f'(2)<f'(1)<a | D. | f'(1)<f'(2)<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com