已知Sn为等比数列{an}的前n项和.公比q=2.S99=154.则a3+a6+a9+-+a99=88．题目和参考答案——青夏教育精英家教网—

19．已知S_n为等比数列{a_n}的前n项和，公比q=2，S₉₉=154，则a₃+a₆+a₉+…+a₉₉=88．

分析公比q=2，S₉₉=154，可得$\frac{{a}_{1}（1-{2}^{99}）}{1-2}$=154，可得${a}_{1}（{2}^{99}-1）$=154．又a₃+a₆+a₉+…+a₉₉=$\frac{{a}_{3}[（{2}^{3}）^{33}-1]}{{2}^{3}-1}$=$\frac{4{a}_{1}（{2}^{99}-1）}{7}$，代入即可得出．

解答解：∵公比q=2，S₉₉=154，∴$\frac{{a}_{1}（1-{2}^{99}）}{1-2}$=154，可得${a}_{1}（{2}^{99}-1）$=154．
则a₃+a₆+a₉+…+a₉₉=$\frac{{a}_{3}[（{2}^{3}）^{33}-1]}{{2}^{3}-1}$=$\frac{4{a}_{1}（{2}^{99}-1）}{7}$=$\frac{4}{7}×154$=88，
故答案为：88．

点评本题考查了等比数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案

自主学语文系列答案

每日10分钟口算心算速算天天练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

12．已知{a_n}是公差为1的等差数列，a₃+a₇=10
（1）求数列{a_n}的通项公式；
（2）设$b_n=2^{a_n}+a_n$，求数列{b_n}的前n项和T_n．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

13．

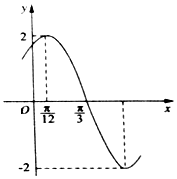已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，下列说法正确的是（　　）

	A．	函数f（x）的图象关于直线x=-$\frac{2π}{3}$对称
	B．	函数f（x）的图象关于点（-$\frac{11π}{12}$，0）对称
	C．	若方程f（x）=m在[-$\frac{π}{2}$，0]上有两个不相等的实数根，则实数m∈（-2，-$\sqrt{3}$]
	D．	将函数f（x）的图象向左平移$\frac{π}{6}$个单位可得到一个偶函数

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点到右焦点的距离为$\sqrt{3}$+$\sqrt{2}$，椭圆上的点到右焦点的距离的最小值为$\sqrt{3}$-$\sqrt{2}$．
（1）求椭圆C的方程；
（2）设斜率为1的直线l经过椭圆上顶点，并与椭圆交于A，B两点，求|AB|．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．已知函数f（x）=ma^x+a^2x-1，（a＞0且a≠1，m∈R）．
（1）若a=$\frac{1}{2}$，m=1时，试判定函数y=f（x）的单调性；
（2）当m=2时，函数y=f（x）在区间x∈[-1，1]上的最大值是14，求实数a的值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．设函数$f（x）=\frac{x^2}{2}-klnx$．
（1）若k∈R，求f（x）的单调区间；
（2）若k＞0，讨论f（x）当$x∈（1，\sqrt{e}）$时的零点的个数．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

11．f（x）=$\frac{1}{2}$mx²+lnx-2x在定义域内单调递增，则实数m取值范围为[1，+∞）．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．$g（x）=x+\frac{1}{x}$上各点处的切线倾斜角为α，则α的取值范围（　　）