
| A. | ρcosθ+ρsinθ=2 | B. | ρcosθ-ρsinθ=2 | C. | ρcosθ+ρsinθ=$\sqrt{2}$ | D. | ρcosθ-ρsinθ=$\sqrt{2}$ |
分析 化参数方程与普通方程,求出圆的圆心与半径,求出切线的斜率,然后求解切线方程,转化为极坐标方程.
解答 解:因为曲线C的参数方程为$\left\{\begin{array}{l}{x=\sqrt{2}cost}\\{y=\sqrt{2}sint}\end{array}\right.$(t为参数),所以其普通方程为x2+y2=2,即曲线C为以原点为圆心,$\sqrt{2}$为半径的圆.
由于点(1,1)在圆上,且该圆过(1,1)点的半径的斜率为1,
所以切线l的斜率为-1,其普通方程为x+y-2=0,
化为极坐标方程为ρcosθ+ρsinθ=2.
故选:A.
点评 本题考查参数方程与普通方程以及极坐标方程的互化,直线与圆的位置关系的应用,考查计算能力.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,⊙O1与⊙O2外切于点P,从⊙O1上点A作的切线AB,切点为B,连AP(不过O1)并延长与⊙O2交于点C.
如图所示,⊙O1与⊙O2外切于点P,从⊙O1上点A作的切线AB,切点为B,连AP(不过O1)并延长与⊙O2交于点C.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
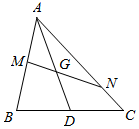 如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB、AC于M、N两点.若$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则$\frac{1}{x}$+$\frac{1}{y}$=4.
如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB、AC于M、N两点.若$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则$\frac{1}{x}$+$\frac{1}{y}$=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2>1,则x>1”的否命题为“若x2>1,则x≤1” | |
| B. | 命题“?x0∈R,x02>1”的否定是“?x∈R,x2>1” | |
| C. | 命题“x≤1是x2+2x-3≤0的必要不充分条件”为假命题 | |
| D. | 命题“若x=y,则cosx=cosy”的逆命题为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com