
分析 先验证n=1时结论成立,假设n=k时结论成立,用n表示出1+2+3+…+k,1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{k}$,代入当n=k+1时的式子进行整理即可得出结论.
解答 证明:当n=1时,1×1=12,结论显然成立,
假设n=k时结论成立,即(1+2+3+…+k)(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{k}$)≥k2,
∴1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{k}$≥$\frac{{k}^{2}}{1+2+3+…+k}$=$\frac{2k}{k+1}$.
∴(1+2+3+…+k+(k+1))(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{k}$+$\frac{1}{k+1}$)=(1+2+3+…+k)(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{k}$)+(1+2+3+…+k)×$\frac{1}{k+1}$+(k+1)(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{k}$)+1.
≥k2+$\frac{k(k+1)}{2}×\frac{1}{k+1}$+(k+1)×$\frac{2k}{k+1}$+1=k2+$\frac{5k}{2}$+1>(k+1)2.
∴当n=k+1时,结论成立.
∴(1+2+3+…+n)(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)≥n2.(n∈N+)
点评 本题考查了数学归纳法的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4\sqrt{5}}{5}$ | D. | $\frac{16}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>4或x<0} | B. | {x|1<x<4} | C. | {x|1<x≤4} | D. | {x|1≤x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<0} | B. | {x|-2<x<2} | C. | {x|-2<x<0} | D. | {x|x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
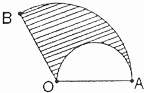 如图,在圆心角为120°的扇形OAB中,以OA为直径作一个半圆,若在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )
如图,在圆心角为120°的扇形OAB中,以OA为直径作一个半圆,若在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )| A. | $\frac{5}{8π}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{8π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$-2 | D. | $\frac{9}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com