
���� ��1��������ɵã�$\left\{\begin{array}{l}{-A+b=100}\\{A+b=500}\end{array}\right.$�����A��b����$\frac{2��}{��}$=2����8-2������æأ��ɵ�y=f��x��=200sin$��\frac{��}{6}x+�գ�$+300����sin$��\frac{��}{6}��2+�գ�$=-1����0��|��|���У���æգ����ɵó���
��2����200sin$��\frac{��}{6}x-\frac{5��}{6}��$+300��400�������������Һ����ĵ�����ֵ�ɵó���
��� �⣺��1��������ɵã�$\left\{\begin{array}{l}{-A+b=100}\\{A+b=500}\end{array}\right.$�����A=200��b=300��
��$\frac{2��}{��}$=2����8-2������æ�=$\frac{��}{6}$��
��y=f��x��=200sin$��\frac{��}{6}x+�գ�$+300��
��sin$��\frac{��}{6}��2+�գ�$=-1����0��|��|���У�
��æ�=$-\frac{5��}{6}$��
��y=f��x��=200sin$��\frac{��}{6}x-\frac{5��}{6}��$+300��
��2����200sin$��\frac{��}{6}x-\frac{5��}{6}��$+300��400��
����sin$��\frac{��}{6}x-\frac{5��}{6}��$$��\frac{1}{2}$����x��N*��1��x��12��
���x=6��7��8��9��10��
���Ӧ����6��7��8��9��10�·�Ҫ��������400�˵��òͣ�
���� ���⿼�������Һ�����ͼ�������ʡ�����ʽ�Ľⷨ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ԲC��x2+3y2=3b2��b��0��
��ͼ����ԲC��x2+3y2=3b2��b��0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 1$+\sqrt{3}$ | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
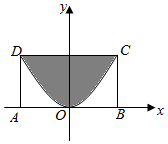 ��ͼ���費��ʽ��$\left\{{\begin{array}{l}{-1��x��1}\\{0��y��1}\end{array}}\right.$��ʾ��ƽ������Ϊ������ABCD��������ABCD�ڵ�����Ϊ������y=x2��һ���֣����ڳ�����ABCD�����ȡһ���㣬��˵�ȡ����Ӱ���ֵĸ��ʵ��ڣ�������
��ͼ���費��ʽ��$\left\{{\begin{array}{l}{-1��x��1}\\{0��y��1}\end{array}}\right.$��ʾ��ƽ������Ϊ������ABCD��������ABCD�ڵ�����Ϊ������y=x2��һ���֣����ڳ�����ABCD�����ȡһ���㣬��˵�ȡ����Ӱ���ֵĸ��ʵ��ڣ�������| A�� | $\frac{2}{3}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-$\frac{1}{x}$ | B�� | y=x3+x | C�� | y=-x|x| | D�� | y=ln$\frac{1+x}{1-x}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com