
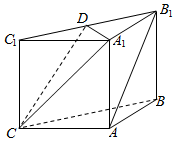
 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.分析 (1)连结AC1交A1C于O点,连结OD,由中位线定理可得OD∥AB1,故而AB1∥平面A1DC;
(2)由正方形的性质得出A1A⊥A1C1,A1A⊥A1B1,故A1A⊥平面A1B1C1,于是CC1⊥平面A1B1C1,得出CC1⊥A1D.又三线合一得出A1D⊥B1C1,故而A1D⊥平面BB1C1C.
解答 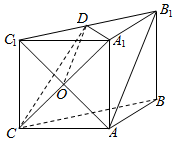 证明:(1)连结AC1交A1C于O点,连结OD,
证明:(1)连结AC1交A1C于O点,连结OD,
∵四边形AA1C1C是正方形,∴O是AC1的中点,
又点D是棱B1C1的中点,
∴OD∥AB1,∵AB1?平面A1DC,OD?平面A1DC,
∴AB1∥平面A1DC.
(2)∵侧面ABB1A1,ACC1A1均为正方形,
∴A1A⊥A1C1,A1A⊥A1B1,又A1C1?平面A1B1C1,A1B1?平面A1B1C1,A1B1∩A1C1=A1,
∴A1A⊥平面A1B1C1,∵AA1∥CC1,
∴CC1⊥平面A1B1C1,∵A1D?平面A1B1C1,
∴CC1⊥A1D.
又∵A1B1=AB=1,A1C1=AC=1,
∴A1B1=A1C1,∵D是B1C1的中点,
∴A1D⊥B1C1,
又CC1?平面BCC1B1,B1C1?平面BCC1B1,CC1∩B1C1=C1,
∴A1D⊥平面BCC1B1.
点评 本题考查了线面平行与垂直的判定,构造平行线或垂线是证明问题的关键,需要掌握几种常用的构造方法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 项目 | 智慧技术 | 智慧产业 | 智慧应用 | 智慧服务 | 智慧治理 | 智慧人文 | 智慧生活 |
| 指标分数x | 6.8 | 7 | 6.8 | 6.8 | 7.2 | 7 | 7.4 |
| 智慧级别y | 9 | 8.8 | 9 | 9.1 | 9.2 | 8.8 | 9.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
| 日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2(x-3) | B. | y=-2(x-3) | C. | y=$\frac{1}{2}$(x-3) | D. | y=-$\frac{1}{2}$(x-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com