
| 项目 | 智慧技术 | 智慧产业 | 智慧应用 | 智慧服务 | 智慧治理 | 智慧人文 | 智慧生活 |
| 指标分数x | 6.8 | 7 | 6.8 | 6.8 | 7.2 | 7 | 7.4 |
| 智慧级别y | 9 | 8.8 | 9 | 9.1 | 9.2 | 8.8 | 9.1 |
分析 (1)根据回归系数公式计算回归系数,得出回归方程;
(2)根据各项指标的分数分布得出ξ的取值情况,计算各种可能的概率得到分布列,代入公式计算数学期望.
解答 解:(1)$\overline{x}$=$\frac{1}{7}×(6.8+7+6.8+6.8+7.2+7+7.4)$=7,
$\overline{y}=\frac{1}{7}×(9+8.8+9+9.1+9.2+8.8+9.1)$=9.
$\sum_{i=1}^{7}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$=0+0+0+(-0.2)×0.1+0.2×0.2+0+0.4×0.1=0.06.
$\sum_{i=1}^{7}({x}_{i}-\overline{x})^{2}$=0.04+0+0.04+0.06+0.04+0+0.16=0.34.
∴$\stackrel{∧}{b}$=$\frac{0.06}{0.34}$=$\frac{3}{17}$.$\stackrel{∧}{a}$=9-$\frac{3}{17}×7$=$\frac{132}{17}$.
∴y关于x的线性回归方程为$\stackrel{∧}{y}$=$\frac{3}{17}x$+$\frac{132}{17}$.
(2)级别在[9.1,10)内的有3项,在区间[9,9.1)内的有两项,在区间[8,9)内的有两项.
∴从中随机抽取2项指标考查,总得分ξ的取值集合为{10,11,12,15,16,20}.
从7项指标中随机抽取两项共有${C}_{7}^{2}$=21个基本事件,
P(ξ=10)=$\frac{{C}_{2}^{2}}{21}=\frac{1}{21}$,P(ξ=11)=$\frac{{C}_{2}^{1}{C}_{2}^{1}}{21}=\frac{4}{21}$,P(ξ=12)=$\frac{{C}_{2}^{2}}{21}=\frac{1}{21}$,
P(ξ=15)=$\frac{{C}_{3}^{1}{C}_{2}^{1}}{21}=\frac{2}{7}$,P(ξ=16)=$\frac{{C}_{3}^{1}{C}_{2}^{1}}{21}=\frac{2}{7}$,P(ξ=20)=$\frac{{C}_{3}^{2}}{21}=\frac{1}{7}$.
∴ξ的分布列为:
| ξ | 10 | 11 | 12 | 15 | 16 | 20 |
| P | $\frac{1}{21}$ | $\frac{4}{21}$ | $\frac{1}{21}$ | $\frac{2}{7}$ | $\frac{2}{7}$ | $\frac{1}{7}$ |
点评 本题考查了回归方程的求解,随机变量的分布列和数学期望,属于中档题.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | $\frac{107}{15}$ | C. | $\frac{219}{31}$ | D. | $\frac{209}{29}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,使用时需要用清水清洗干净,如表是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的统计表:
菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,使用时需要用清水清洗干净,如表是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的统计表:| x | 1 | 2 | 3 | 4 | 5 |
| y | 58 | 54 | 39 | 29 | 10 |
| ω | 1 | 4 | 9 | 16 | 25 |
| y | 58 | 54 | 39 | 29 | 10 |
| ωi-$\overline{ω}$ | |||||
| yi-$\overline{y}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
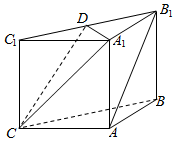 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | m-26 | 38 | 66+n |
| A. | 增加4度 | B. | 降低4度 | C. | 增加120度 | D. | 降低120度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 2e | D. | 2e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “至少有1个正面朝上”,“都是反面朝上” | |
| B. | “至少有1个正面朝上”,“至少有1个反面朝上” | |
| C. | “恰有1个正面朝上”,“恰有2个正面朝上” | |
| D. | “至少有1个反面朝上”,“都是反面朝上” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com