
分析 (1)首项为1的正项数列{an}满足an+12+an2<$\frac{5}{2}{a_{n+1}}{a_n}$,n∈N*,化为(2an+1-an)(an+1-2an)<0,解得:$\frac{1}{2}<\frac{{a}_{n+1}}{{a}_{n}}$<2.又a2=$\frac{3}{2}$,a3=x,a4=4,代入解出即可得出.
(2)由于首项为1的正项数列{an},由于$\frac{1}{2}<\frac{{a}_{n+1}}{{a}_{n}}$<2.可得$\frac{1}{2}<q<2$.对q分类讨论:q=1时,n=1时不满足条件,因此q≠1.②由$\frac{1}{2}•\frac{1-{q}^{n}}{1-q}$$<\frac{1-{q}^{n+1}}{1-q}$<2$•\frac{1-{q}^{n}}{1-q}$,$\frac{1}{2}$<q<1时,经过验证成立:$\frac{1}{2}$<q<1.2>q>1时,化为2qn+1-qn-1>0,qn+1-2qn+1<0不成立,舍去.
(3)设首项为1的正项数列{an}的公差为d,d≥0,由$\frac{1}{2}<\frac{{a}_{n+1}}{{a}_{n}}$<2,化为1+(n-1)d<2(1+nd)<4[1+(n-1)d].分类讨论:n=1时,n=2时,n≥3时,可得:0≤d<1.根据a1,a2,…,ak(k≥3)成等差数列,a1+a2+…+ak=120,可得k+$\frac{k(k-1)}{2}$d=120,k=1时,不成立,舍去.k≥2时,解得d=$\frac{240-2k}{{k}^{2}-k}$,代入解得:15<k≤120.即可得出.
解答 解:(1)∵首项为1的正项数列{an}满足an+12+an2<$\frac{5}{2}{a_{n+1}}{a_n}$,n∈N*,化为(2an+1-an)(an+1-2an)<0,
∴$\frac{1}{2}<\frac{{a}_{n+1}}{{a}_{n}}$<2.
又a2=$\frac{3}{2}$,a3=x,a4=4,
∴$\frac{1}{2}<\frac{2x}{3}<2$,$\frac{1}{2}<\frac{4}{x}<2$,
解得:2<x<3.
∴x的取值范围是(2,3).
(2)由于首项为1的正项数列{an},
∵$\frac{1}{2}<\frac{{a}_{n+1}}{{a}_{n}}$<2.∴$\frac{1}{2}<q<2$.
①q=1时,n=1时不满足:$\frac{1}{2}{S_n}$<Sn+1<2Sn,n∈N*,因此q≠1.
②可得$\frac{1}{2}•\frac{1-{q}^{n}}{1-q}$$<\frac{1-{q}^{n+1}}{1-q}$<2$•\frac{1-{q}^{n}}{1-q}$,
$\frac{1}{2}$<q<1时,化为2qn+1-qn<1,qn+1-2qn+1>0,由于qn(2q-1)<1,因此2qn+1-qn<1恒成立;由qn<q,可得q2n<qn+1,∴qn$<\sqrt{{q}^{n+1}}$,∴2qn$<2\sqrt{{q}^{n+1}}$<1+qn+1,因此qn+1-2qn+1>0恒成立,可得:$\frac{1}{2}$<q<1.
2>q>1时,化为2qn+1-qn-1>0,qn+1-2qn+1<0,无解,舍去.
综上可得:$\frac{1}{2}$<q<1.
(3)设首项为1的正项数列{an}的公差为d,d≥0,
由$\frac{1}{2}<\frac{{a}_{n+1}}{{a}_{n}}$<2,可得$\frac{1}{2}$<$\frac{1+nd}{1+(n-1)d}$<2,
化为1+(n-1)d<2(1+nd)<4[1+(n-1)d],
n=1时,0≤d<1;n=2时,d≥0;
n≥3时,d≥0.
综上可得:0≤d<1.
∵a1,a2,…,ak(k≥3)成等差数列,a1+a2+…+ak=120,
∴k+$\frac{k(k-1)}{2}$d=120,
k=1时,不成立,舍去.
k≥2时,解得d=$\frac{240-2k}{{k}^{2}-k}$,
∵0≤d<1.
∴0≤$\frac{240-2k}{{k}^{2}-k}$<1.
解得:15<k≤120.
∴满足条件的正整数k的最小值为16,此时d=$\frac{13}{15}$,
相应数列的通项公式为:an=1+$\frac{13}{15}$(n-1)=$\frac{13n+2}{15}$.
数列为:1,$\frac{28}{15}$,…,14.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、不等式的解法,考查了分类讨论方法推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{49}{128}$ | C. | $\frac{81}{128}$ | D. | $\frac{125}{128}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上一年出险次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 下一年保费倍率 | 85% | 100% | 125% | 150% | 175% | 200% |
| 连续两年没出险打7折,连续三年没出险打6折 | ||||||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
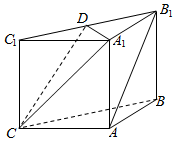 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点D是△ABC的边BC上一点,且AC=$\sqrt{3}$AD,$\sqrt{3}$CD=2AC,CD=2BD.
如图,点D是△ABC的边BC上一点,且AC=$\sqrt{3}$AD,$\sqrt{3}$CD=2AC,CD=2BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com