
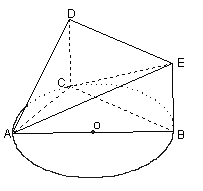
 平面ABC ,
平面ABC ,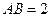 ,
,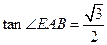 .
. 平面
平面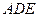 ;
;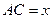 ,
,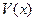 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求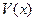 的表达式;
的表达式;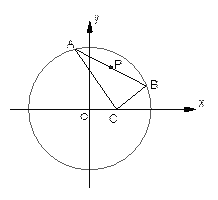
 (3)当
(3)当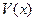 取得最大值时,求证:AD=CE.
取得最大值时,求证:AD=CE.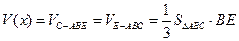
 (
(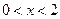 )
)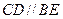 ,
, ---------1分
---------1分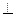 平面ABC ,
平面ABC , 平面ABC ∴
平面ABC ∴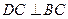 . ----------2分
. ----------2分 且
且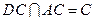
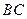
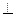 平面ADC.
平面ADC. 
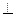 平面ADC ---------------------------------------3分
平面ADC ---------------------------------------3分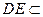 平面ADE ∴平面ACD
平面ADE ∴平面ACD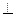 平面
平面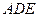 ----------------4分
----------------4分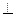 平面ABC , CD//BE ∴
平面ABC , CD//BE ∴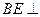 平面ABC
平面ABC 平面
平面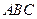 ∴BE
∴BE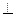 AB, --------------------------------------------------------5分
AB, --------------------------------------------------------5分 ,
,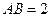 得
得 ------------6分
------------6分 (
(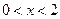 )
)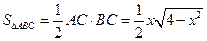 ------------------------------------7分
------------------------------------7分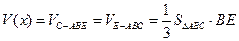
 (
(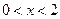 )-------8分
)-------8分 (3)由(2)知要
(3)由(2)知要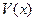 取得最大值,当且仅当
取得最大值,当且仅当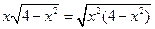 取得最大值,
取得最大值,
 ∵
∵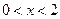 ∴
∴ ------------10分
------------10分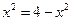 ,即
,即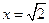 时,“=”成立,
时,“=”成立,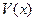 取得最大值时
取得最大值时 ,这时△ACB为等腰直角三角形
,这时△ACB为等腰直角三角形 ≌
≌ ------------------12分
------------------12分 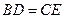
 ∴AD=CE------------------------------------------------------------14分
∴AD=CE------------------------------------------------------------14分

科目:高中数学 来源:不详 题型:解答题
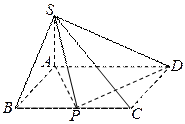 如图,四棱锥
如图,四棱锥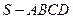 的底面是矩形,
的底面是矩形,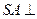 底面
底面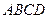 ,P为BC边的中点,SB与
,P为BC边的中点,SB与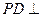 平面SAP;
平面SAP;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
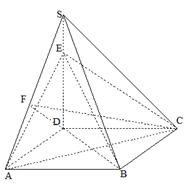 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.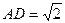 ,E是SD上的点.(Ⅰ)求证:AC⊥BE;
,E是SD上的点.(Ⅰ)求证:AC⊥BE;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
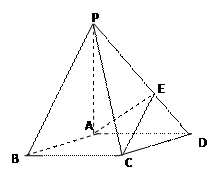 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=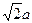 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.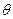 的大小.
的大小.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
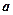 、
、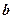 及平面
及平面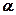 ,给出四个下列命题:
,给出四个下列命题: ,
,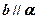 ,则
,则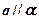 ;
;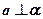 ,
,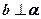 ,则
,则 ;
;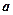 、
、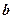 与
与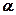 所成的角相等,则
所成的角相等,则 ;
;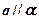 ,
,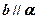 ,则
,则 .
.A. 个 个 | B. 个 个 | C. 个 个 | D.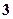 个 个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
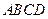 --
--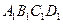 ,E、F分别是
,E、F分别是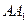 、
、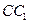 的中点,p是
的中点,p是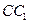 上的动点(包括端点),过E、D、P作正方体的截面,若截面为四边形,则P的轨迹是
上的动点(包括端点),过E、D、P作正方体的截面,若截面为四边形,则P的轨迹是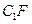 B、线段
B、线段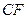 C、线段
C、线段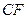 和一点
和一点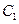 D、线段
D、线段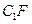 和一点C。
和一点C。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com