
分析 (1)利用三角恒等变换的应用化简f(x)=(sinx-t)2+t2-6t+1,分t<-1、-1≤t≤1、t>1三类讨论,可分别求得f(x)的最小值g(t),从而可得g(t)的表达式;
(2)依题意知,关于t的方程 t2-6t+1-kt=0 在(-1,1)内有且只有一个实根.分①当△=(6+k)2-4=0时,应有-1<$\frac{6+k}{2}$<1,与②当△=(6+k)2-4>0时,应有(k+8)(-k-4)<0,从而可得实数k的取值范围.
解答 解:(1)f(x)=-cos2x-4t•sin$\frac{x}{2}$cos$\frac{x}{2}$+2t2-6t+2
=sin2x-2t•sinx+2t2-6t+1=(sinx-t)2+t2-6t+1,
当t<-1时,则当sinx=-1时,f(x)取得最小值g(t)=(-1-t)2+t2-6t+1=2t2-4t+2.
当-1≤t≤1时,则当sinx=t时,f(x)的最小值g(t)=t2-6t+1.
当t>1时,则当sinx=1时,f(x)的最小值g(t)=(1-t)2+t2-6t+1=2t2-8t+2.
综上,g(t)=$\left\{\begin{array}{l}{{2t}^{2}-4t+2,t<-1}\\{{t}^{2}-6t+1,-1≤t≤1}\\{{2t}^{2}-8t+2,t>1}\end{array}\right.$.
(3)当-1<t<1时,关于t的方程g(t)=kt
即t2-6t+1=kt有且仅有一个实根?关于t的方程 t2-6t+1-kt=0 在(-1,1)内有且只有一个实根,
①当△=(6+k)2-4=0时,应有-1<$\frac{6+k}{2}$<1,解得 k∈∅.
②当△=(6+k)2-4>0时,即 k<-8,或k>-4时,
令h(t)=t2-6t+1-kt,由题意可得 h(-1)h(1)=(k+8)(-k-4)<0,解得 k<-8,或 k>-4.
综合①②可得,当k<-8,或 k>-4 时,关于t的方程g(t)=kt有且只有一个实根.
故所求的实数k的取值范围为(-∞,-8)∪(-4,+∞).
点评 本题考查根的存在性根的个数判断,突出考查分类讨论思想、等价转化思想与函数方程思想的综合运用,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [0,1] | C. | [-2,2] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | c>b>a | C. | b>c>a | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
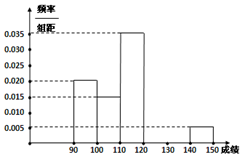 某班高三期中考试后,对考生的数学成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].得到频率分布直方图如图所示,若第四、五、六组的人数依次成等差数列,且第六组有2人
某班高三期中考试后,对考生的数学成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].得到频率分布直方图如图所示,若第四、五、六组的人数依次成等差数列,且第六组有2人查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com