
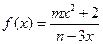 是定义域上的奇函数,且
是定义域上的奇函数,且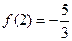 ;函数
;函数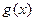 是
是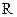 上的增函数,
上的增函数,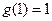 且对任意
且对任意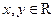 ,总有
,总有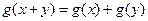
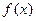 的解析式;
的解析式;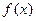 在
在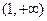 上的单调性,并加以证明;
上的单调性,并加以证明;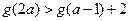 ,求实数
,求实数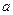 的取值范围.
的取值范围.科目:高中数学 来源:不详 题型:解答题
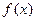 满足:对定义域内任意两个不相等的实数
满足:对定义域内任意两个不相等的实数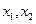 ,都有,则称函数
,都有,则称函数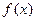 为H函数.已知
为H函数.已知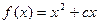 ,且
,且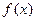 为偶函数.
为偶函数.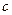 的值;
的值;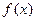 为H函数;
为H函数;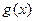 ,并说明理由.
,并说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
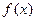 的边际函数为
的边际函数为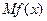 ,定义为
,定义为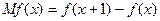 ,某服
,某服 件的收入函数为
件的收入函数为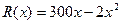 (单位元),其成本函数为
(单位元),其成本函数为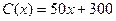 (单位元),利润等于收入与成本之差.
(单位元),利润等于收入与成本之差.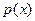 及其边际利润函数
及其边际利润函数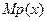 ;
;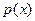 及其边际利润函数
及其边际利润函数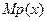 的最大值;
的最大值;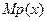 最大值的实际意义是什么?
最大值的实际意义是什么?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.m < a < b < n | B.a < m < n < b |
| C.a < m < b < n | D.m < a < n < b |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
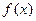 是定义在
是定义在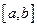 上的函数,其图像是一条连续的曲线,且满足下列条件:
上的函数,其图像是一条连续的曲线,且满足下列条件: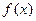 的值域为G,且
的值域为G,且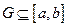 ;
;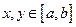 ,都有
,都有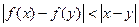 .
.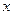 的方程
的方程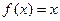 在区间
在区间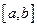 上根的情况是 ( ▲ )
上根的情况是 ( ▲ )| A.没有实数根 | B.有且仅有一个实数根 |
| C.恰有两个实数根 | D.有无数个不同的实数根 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
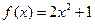 ,值域为
,值域为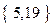 的“孪生函数”共有_______个.
的“孪生函数”共有_______个.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com