Question

【题目】已知点A（1， ）在椭圆E： =1上，若斜率为 的直线l与椭圆E交于B，C两点，当△ABC的面积最大时，求直线l的方程．

Answer 1

【答案】解：设直线l的方程为y= x+m，设B（x1 ， y1），C（x2 ， y2），
由 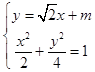，消去y，整理得4x2+2 mx+m2﹣4=0，
则△=8m2﹣16（m2﹣4）=8（8﹣m2）＞0，解得：0≤m2＜8，
由韦达定理可知：x1+x2=﹣ ，x1x2= ，
由弦长公式可知：丨BC丨= = ，
又点A到l的距离为d= = ，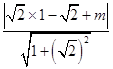
故S△ABC= 丨BC丨d= = ≤ = ，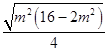
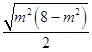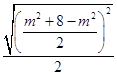当且仅当 m2=8﹣m2 ， 即m=±2时取等号，此时满足0≤m2＜8，
故直线l的方程为y= x±2．
【解析】由题意可知：设直线l的方程为y= x+m，代入椭圆方程，由△＞0，求得0≤m2＜8，根据韦达定理及弦长公式求得丨BC丨，由点到直线的距离公式点A到l的距离为d，再利用三角形的面积公式求得S△ABC= 丨BC丨d，利用基本不等式的性质即可求得△ABC的面积最大值时，m的取值，即可求得直线l的方程．