
����Ŀ��Ϊ�˼��ij�ֲ�Ʒ����������λ��ǧ�ˣ�����ȡ��һ������ΪN�������������õ�������������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ��ͼ��
���� | Ƶ�� | Ƶ�� |
[17.5��20�� | 10 | 0.05 |
[20��225�� | 50 | 0.25 |
[22.5��25�� | a | b |
[25��27.5�� | 40 | c |
[27.5��30] | 20 | 0.10 |
�ϼ� | N | 1 |
�����������N��a��b��c��ֵ��
������Ƶ�ʷֲ�ֱ��ͼ��d��ֵ��
���Ӹò�Ʒ�������ȡһ�����Թ��������Ʒ����������25ǧ�˵ĸ��ʣ�
���𰸡��⣺������Ƶ�ʷֲ����ã� 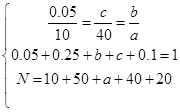 ��
��
���N=200��a=80��b=0.4��c=0.2��
������Ƶ�ʷֲ�����[25��27.5��Ƶ��Ϊ0.2��
��d= ![]() =0.08��
=0.08��
������Ƶ�ʷֲ���֪��Ʒ������������25ǧ�˵�Ƶ��Ϊ0.2+0.1=0.3��
��Ӹò�Ʒ�������ȡһ����
���������Ʒ����������25ǧ�˵ĸ���p=1��0.3=0.7��
��������������Ƶ��= ![]() ����Ƶ�ʷֲ������������N��a��b��c��ֵ��������Ƶ�ʷֲ�����[25��27.5��Ƶ��Ϊ0.2���ɴ������Ƶ�ʷֲ�ͼ�е�d��ֵ��������Ƶ�ʷֲ���֪��Ʒ������������25ǧ�˵�Ƶ��Ϊ0.2+0.1=0.3���Ӹò�Ʒ�������ȡһ�����ɴ��ܹ��������Ʒ����������25ǧ�˵ĸ��ʣ�
����Ƶ�ʷֲ������������N��a��b��c��ֵ��������Ƶ�ʷֲ�����[25��27.5��Ƶ��Ϊ0.2���ɴ������Ƶ�ʷֲ�ͼ�е�d��ֵ��������Ƶ�ʷֲ���֪��Ʒ������������25ǧ�˵�Ƶ��Ϊ0.2+0.1=0.3���Ӹò�Ʒ�������ȡһ�����ɴ��ܹ��������Ʒ����������25ǧ�˵ĸ��ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=�� ![]() sinx
sinx ![]() cosx+1 ��������f��x������С�����ں͵����������䣻
cosx+1 ��������f��x������С�����ں͵����������䣻
������x��[0�� ![]() ]����f��x��=
]����f��x��= ![]() ����cosx��ֵ��
����cosx��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����p������x2+y2��ax+y+1=0��ʾԲ������q������2ax+��1��a��y+1=0��ʾб�ʴ���1��ֱ�ߣ���p��qΪ�����⣬p��qΪ�����⣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��F1 �� F2��˫����C�� ![]() ��a��0��b��0�������ҽ��㣬��F1��ֱ��l��C��������֧�ֱ���A��B���㣮����ABF2Ϊ�ȱ������Σ���˫���ߵ�������Ϊ�� ��
��a��0��b��0�������ҽ��㣬��F1��ֱ��l��C��������֧�ֱ���A��B���㣮����ABF2Ϊ�ȱ������Σ���˫���ߵ�������Ϊ�� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��1�� ![]() ������ԲE��
������ԲE�� ![]() =1�ϣ���б��Ϊ
=1�ϣ���б��Ϊ ![]() ��ֱ��l����ԲE����B��C���㣬����ABC��������ʱ����ֱ��l�ķ��̣�
��ֱ��l����ԲE����B��C���㣬����ABC��������ʱ����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����p��x2��3x��4��0������q��x2��6x+9��m2��0����p��q�ij�ֲ���Ҫ��������m��ȡֵ��Χ�ǣ� ��
A.[��1��1]
B.[��4��4]
C.�����ޣ���1]��[1��+�ޣ�
D.�����ޣ���4]��[4��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪p��x��R��cos2x��sinx+2��m��q������ ![]() ��[1��+�ޣ��ϵ����ݼ���
��[1��+�ޣ��ϵ����ݼ���
��I����p��qΪ�����⣬��m��ȡֵ��Χ��
��II����p��qΪ�����⣬p��qΪ�����⣬��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ABC=90�㣬AB= ![]() ��BC=1��PΪ��ABC��һ�㣬��BPC=90�㣮
��BC=1��PΪ��ABC��һ�㣬��BPC=90�㣮 
��1����PB= ![]() ����PA��
����PA��
��2������APB=150�㣬��tan��PBA��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c����acosC��bcosB��ccosA�ɵȲ����У�
��1�����B�Ĵ�С��
��2����2sin2A+cos��A��C����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com