
分析 (1)求出双曲线的标准方程求出焦点坐标,利用直线和圆相交的弦长公式进行求解即可.
(2)根据|PD|,|PO|,|PE|成等比数列,建立方程关系,结合向量数量积的坐标进行化简求解即可.
解答 解:(1)双曲线的标准方程为$\frac{{y}^{2}}{\frac{1}{2}}-\frac{{x}^{2}}{\frac{1}{2}}$=1,则c=$\sqrt{\frac{1}{2}+\frac{1}{2}}=\sqrt{1}$=1,
即双曲线的焦点C(0,1),
圆心C到直线3x+4y+1=0的距离d=$\frac{|0+4+1|}{5}=\frac{5}{5}=1$,
则半径r=$\sqrt{{1}^{2}+{2}^{2}}=\sqrt{5}$.故圆C的标准方程为x2+(y-1)2=5.
(2)设P(x,y),∵|PD|,|PO|,|PE|成等比数列,
∴$\sqrt{(x+2)^{2}+{y}^{2}}$•$\sqrt{(x-2)^{2}+{y}^{2}}$=x2+y2,
整理得x2-y2=2,
故$\overrightarrow{PD}$•$\overrightarrow{PE}$=(-2-x,-y)•(2-x,-y)=x2-4+y2=2(y2-1),
由于P在圆C内,则$\left\{\begin{array}{l}{{x}^{2}+(y-1)^{2}<5}\\{{x}^{2}-{y}^{2}=2}\end{array}\right.$,
得y2-y-1<0,得$\frac{1-\sqrt{5}}{2}$<y<$\frac{1+\sqrt{5}}{2}$,
则0≤y2<($\frac{1+\sqrt{5}}{2}$)2=$\frac{3+\sqrt{5}}{2}$,
∴2(y2-1)∈[-2,1+$\sqrt{5}$),
则$\overrightarrow{PD}$•$\overrightarrow{PE}$的取值范围是[-2,1+$\sqrt{5}$).
点评 本题主要考查双曲线性质的综合应用以及向量数量积的应用,利用方程思想以及转化法是解决本题的关键.考查学生的转化能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 55 | B. | 52 | C. | 39 | D. | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
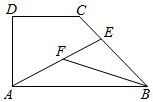 如图,在直角梯形ABCD中,AB=2AD=2DC=2,E为BC边上一点,$\overrightarrow{BC}$=3$\overrightarrow{EC}$,F为线段AE的中点,则$\overrightarrow{AE}$•$\overrightarrow{BF}$=$-\frac{14}{9}$.
如图,在直角梯形ABCD中,AB=2AD=2DC=2,E为BC边上一点,$\overrightarrow{BC}$=3$\overrightarrow{EC}$,F为线段AE的中点,则$\overrightarrow{AE}$•$\overrightarrow{BF}$=$-\frac{14}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | [0,2] | C. | {0,1,2} | D. | {0,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com