
| A. | $\overrightarrow{AB}$=$\overrightarrow{DC}$ | B. | $\overrightarrow{AD}$+$\overrightarrow{AB}$=2$\overrightarrow{AO}$ | C. | $\overrightarrow{AD}$+$\overrightarrow{CB}$=$\overrightarrow 0$ | D. | $\overrightarrow{AB}$-$\overrightarrow{AD}$=$\overrightarrow{BD}$ |
分析 可画出图形,根据平行四边形的定义,及对角线的关系,以及相等向量的概念,向量加法的平行四边形法则,向量加法、减法和数乘的几何意义,便可判断每个选项结论的正误,从而找出正确选项.
解答 解:如图,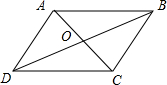
A.AB∥DC,且AB=DC,∴$\overrightarrow{AB}=\overrightarrow{DC}$,即该结论正确;
B.$\overrightarrow{AD}+\overrightarrow{AB}=\overrightarrow{AC}=2\overrightarrow{AO}$,∴该结论正确;
C.$\overrightarrow{AD}+\overrightarrow{CB}=\overrightarrow{AD}+\overrightarrow{DA}=\overrightarrow{0}$,∴该结论正确;
D.根据向量减法的几何意义,$\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DB}$,∴该结论错误.
故选D.
点评 考查平行四边形的定义,清楚平行四边形的对角线互相平分,向量加法、减法和数乘的几何意义,向量加法的平行四边形法则,以及相等向量和相反向量的定义.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
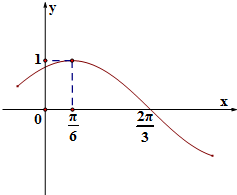 已知函数f(x)=Asin(ωx+φ)(-$\frac{π}{2}$<φ<$\frac{π}{2}$,ω>0,A>0)其部分图象如图所示:
已知函数f(x)=Asin(ωx+φ)(-$\frac{π}{2}$<φ<$\frac{π}{2}$,ω>0,A>0)其部分图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D、E分别为棱CC1、B1C1的中点,
如图,直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D、E分别为棱CC1、B1C1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
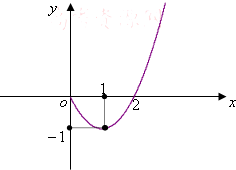 已知二次函数y=f(x)在[0,+∞)上的图象如图所示,顶点坐标为(1,-1).
已知二次函数y=f(x)在[0,+∞)上的图象如图所示,顶点坐标为(1,-1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com