
【题目】如图,三棱锥P-ABC中,PA![]() 平面ABC,
平面ABC,![]()

(1)(Ⅰ)求三棱锥P-ABC的体积;
(2)(Ⅱ)证明:在线段PC上存在点M,使得AC![]() BM,并求
BM,并求![]() 的值.
的值.
【答案】
(1)
![]()
(2)
![]()
【解析】(I)由题设AB=1,AC=2,![]() ,可得
,可得![]() .由PA
.由PA![]() 平面ABC,可知PA是三棱锥P-ABC的高,体积
平面ABC,可知PA是三棱锥P-ABC的高,体积![]() .
.
(II)证:在平面ABC内,过点B作BN![]() AC,垂足为N,过N作MN//PA交PC于M,连接BM,由PA
AC,垂足为N,过N作MN//PA交PC于M,连接BM,由PA![]() 面ABC知PA
面ABC知PA![]() AC,所以MN
AC,所以MN![]() AC,由于BN
AC,由于BN![]() MN=N,故AC
MN=N,故AC![]() 面MBN,又BM
面MBN,又BM![]() 面MBN,所以AC
面MBN,所以AC![]() BM.
BM.
在直角![]() BAN中,AN=AB
BAN中,AN=AB![]() ,从而NC=AC-AN=
,从而NC=AC-AN=![]() ,由MN//PA,得
,由MN//PA,得![]() .
.
【考点精析】认真审题,首先需要了解向量语言表述线面的垂直、平行关系(要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可;设直线![]() 的方向向量是
的方向向量是![]() ,平面
,平面![]() 内的两个相交向量分别为
内的两个相交向量分别为![]() ,若
,若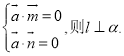 ).
).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(2015·四川)已知函数f(x)=-2(x+a)lnx+x2-2ax-2a2+a,其中a>0.
(1)设g(x)是f(x)的导函数,评论g(x)的单调性;
(2)证明:存在a![]() (0,1),使得f(x)≥0,在区间(1,+
(0,1),使得f(x)≥0,在区间(1,+![]() )内恒成立,且f(x)=0在(1,+
)内恒成立,且f(x)=0在(1,+![]() )内有唯一解.
)内有唯一解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛
(1)求应从这三个协会中分别抽取的运动员人数
(2)将抽取的6名运动员进行编号,编号分别为![]() ,从这6名运动员中随机抽取2名参加双打比赛.(1)用所给编号列出所有可能的结果;(2)设
,从这6名运动员中随机抽取2名参加双打比赛.(1)用所给编号列出所有可能的结果;(2)设![]() 为事件“编号为
为事件“编号为![]() 的两名运动员至少有一人被抽到”,求事件
的两名运动员至少有一人被抽到”,求事件![]() 发生的概率
发生的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.求:(1)现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在[7,8]的概率;(2)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.求:(1)现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在[7,8]的概率;(2)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
组号 | 分组 | 频数 |
1 | [4,5) | 2 |
2 | [5,6) | 8 |
3 | [6,7) | 7 |
4 | [7,8] | 3 |
(1)现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在[7,8]的概率;
(2)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V-ABC中,平面VAB![]() 平面ABC,
平面ABC,![]() VAB为等比三角形,AC
VAB为等比三角形,AC![]() BC且AC=BC=
BC且AC=BC=![]() ,O,M分别为AB,VA的中点。
,O,M分别为AB,VA的中点。
(I)求证:VB//平面MOC;
(II)求证:平面MOC![]() 平面VAB;
平面VAB;
(III)求三棱锥V-ABC的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一直函数![]() ,其中
,其中![]()
(1)讨论![]() 的单调性
的单调性
(2)设曲线![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,曲线在点
,曲线在点![]() 处的切线方程为
处的切线方程为![]() ,求证:对于任意的正实数
,求证:对于任意的正实数![]() ,都有
,都有![]()
(3)若关于![]() 的方程
的方程![]() (
(![]() 为实数)有两个正实根
为实数)有两个正实根![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知2件次品和3件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所 需要的检测费用(单位:元),求X的分布列和均值(数学期望).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C: ![]() +
+ ![]() =1,直线l:
=1,直线l: ![]() (t为参数)
(t为参数)
(1)写出曲线C的参数方程,直线l的普通方程.
(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com