
分析 由$k\overrightarrow a+\overrightarrow b$与$k\overrightarrow a-\overrightarrow b$垂直,得到($k\overrightarrow{a}+\overrightarrow{b}$)($k\overrightarrow{a}-\overrightarrow{b}$)=${k}^{2}{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}$=2k2-25=0,由此能求出实数k.
解答 解:∵两个平面向量$\overrightarrow a,\overrightarrow b$满足$\overrightarrow a=(1,1)$,$\overrightarrow b=(3,4)$,
$k\overrightarrow a+\overrightarrow b$与$k\overrightarrow a-\overrightarrow b$垂直,
∴($k\overrightarrow{a}+\overrightarrow{b}$)($k\overrightarrow{a}-\overrightarrow{b}$)=${k}^{2}{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}$=2k2-25=0,
解得实数k=$±\frac{5\sqrt{2}}{2}$.
故答案为:$±\frac{5\sqrt{2}}{2}$.
点评 本题考查实数值的求法,涉及到平面向量坐标运算法则、向量垂直等基础知识,考查运算求解能力,考查化归与转化思想,是基础题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
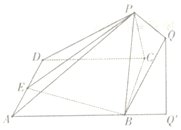 已知如图所示的几何体中,四边形ABCD是边长为2的菱形,面PBC⊥面A BCD,点E是AD 的中点,PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2
已知如图所示的几何体中,四边形ABCD是边长为2的菱形,面PBC⊥面A BCD,点E是AD 的中点,PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
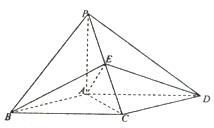
 如图,在多面体ABCDEF中,正三角形BCE所在平面与菱形ABCD所在的平面垂直,FD⊥平面ABCD,且$BC=4,FD=2\sqrt{3}$.
如图,在多面体ABCDEF中,正三角形BCE所在平面与菱形ABCD所在的平面垂直,FD⊥平面ABCD,且$BC=4,FD=2\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com