
 Ϊ����Ӧ���С������˾Ӹ۳ǣ��������������ij�������ſ�չ�ԡ��ذ�ľ��Ϫ������ĸ�ӡ�Ϊ����Ļ������������ľ��Ϫ�����Ӷηֳ�10�Σ�����֯����ɲ�ְ����ÿһ�ε��ϡ����������л����ۺϲ������õ���ֵ���������
Ϊ����Ӧ���С������˾Ӹ۳ǣ��������������ij�������ſ�չ�ԡ��ذ�ľ��Ϫ������ĸ�ӡ�Ϊ����Ļ������������ľ��Ϫ�����Ӷηֳ�10�Σ�����֯����ɲ�ְ����ÿһ�ε��ϡ����������л����ۺϲ������õ���ֵ���������| �ϰ� | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
| ���� | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
���� ��1�������оٷ������10������ȡһ�εĻ����¼���10������A��ʾ����ͬһ���������������־�Ϊ���������¼��������з����A�����Ļ����¼��������ɴ��������ͬһ���������������־�Ϊ�����ĸ��ʣ�
��2�����ݱ������ݣ�����ɾ�Ҷͼ��
��3���ֱ�����ϰ�10�εķ�ֵ���ݵ���λ����ƽ�����ͱ���10�η�ֵ���ݵ���λ����ƽ�������ɴ˿��������������ã�
��� �⣺��1����10������ȡһ�εĻ����¼���10�����ֱ�Ϊ��
��77��72������92��87������84��78������86��83������74��83����
��76��85������81��75������71��89������85��90������87��95����
��Щ�����¼��ǵȿ��ܵģ�
��A��ʾ����ͬһ���������������־�Ϊ���������¼���
��A�����Ļ����¼�Ϊ��
��92��87������86��83������85��90������87��95������4����
��P��A��=$\frac{4}{10}=\frac{2}{5}$��
��2�����ݱ������ݣ�������о�Ҷͼ��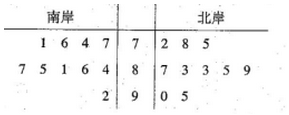
��3���ϰ�10�εķ�ֵ���ݵ���λ��Ϊ��z1=$\frac{81+84}{2}$=82.5��
�ϰ�10�η�ֵ���ݵ�ƽ����Ϊ��
$\overline{{x}_{1}}=\frac{��70��4+1+4+6+7��+��80��5+1+4+5+6+7��+92}{10}$=81.3��
����10�η�ֵ���ݵ���λ��Ϊ��z2=$\frac{83+85}{2}=84$��
����10�η�ֵ���ݵ�ƽ������
$\overline{{x}_{2}}$=$\frac{��70��3+2+5+8��+��80��5+3+3+5+7+9��+��90��2+0+5��}{10}$=83.7��
��z1��z2��$\overline{{x}_{1}}��\overline{{x}_{2}}$�����Կ��������������ã�
���� ������Ҫ���龥Ҷͼ����λ����ƽ�������ŵ���͵Ȼ���֪ʶ������ѧ��Ӧ����ʶ������������������ݴ�����������������������������������˷���������˼�롢��Ȼ���Ȼ����ѧ˼�룮


 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7��/�� | B�� | 6��/�� | C�� | 5��/�� | D�� | 8��/�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x��R��f��x����f��x0�� | B�� | ?x��R��f��x����f��x0�� | C�� | ?x��R��f��x����f��x0�� | D�� | ?x��R��f��x����f��x0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABC-DEF�У�����ABED�DZ߳�Ϊ2�����Σ��ҡ�ABE=$\frac{��}{3}$��BC=$\frac{\sqrt{21}}{2}$����F��ƽ��ABED�ڵ���ͶӰΪG����G��AE�ϣ�FG=$\sqrt{3}$����M���߶�CF�ϣ���CM=$\frac{1}{4}$CF��
��ͼ��������ABC-DEF�У�����ABED�DZ߳�Ϊ2�����Σ��ҡ�ABE=$\frac{��}{3}$��BC=$\frac{\sqrt{21}}{2}$����F��ƽ��ABED�ڵ���ͶӰΪG����G��AE�ϣ�FG=$\sqrt{3}$����M���߶�CF�ϣ���CM=$\frac{1}{4}$CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
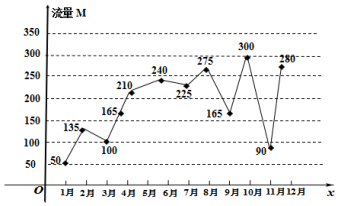 ij�˵��ֻ�ʹ�õ���ÿ��300M�����ײͣ���ͼ��¼��ij����ȥ��1�µ�12�µ�����ʹ����������к�������·ݣ��������������
ij�˵��ֻ�ʹ�õ���ÿ��300M�����ײͣ���ͼ��¼��ij����ȥ��1�µ�12�µ�����ʹ����������к�������·ݣ���������������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com